„Laboratórium 2 - 8. Mérés ellenőrző kérdései” változatai közötti eltérés
| 17. sor: | 17. sor: | ||
==4. Mi lesz állapot-visszacsatolás esetén a zárt rendszer karakterisztikus egyenlete? == | ==4. Mi lesz állapot-visszacsatolás esetén a zárt rendszer karakterisztikus egyenlete? == | ||
| − | Folytonos időben a szakasz állapotegyenlete <math>\dot{x}=Ax + Bu</math>, a zárt rendszer állapotegyenlete, a zárt rendszer karakterisztikus egyenlete pedig | + | Folytonos időben a szakasz állapotegyenlete <math>\dot{x}=Ax + Bu</math>, a zárt rendszer állapotegyenlete <math>\dot{x}=(A-BK) \cdot x</math>, a zárt rendszer karakterisztikus egyenlete pedig <math>\varphi_c(s)=det(sI-(A-BK))</math>. Diszkrét időben a szakasz állapotegyenlete <math>x_{i+1}=\Phi \cdot x_i + \Gamma \cdot u_i</math>, a zárt rendszer állapotegyenlete <math>x_{i+1}=(\Phi-\Gamma K) \cdot x_i</math>, a zárt rendszer állapotegyenlete pedig <math>\varphi_c(z)=(zI-(\Phi - \GammaK))</math>. A pólusáthelyezési feladatban előírjuk a zárt rendszer karakterisztikus egyenletét (ami ekvivalens a zárt rendszer pólusainak, azaz a velük megegyező sajátértékeknek az előírásával), és keressük az ehhez szükséges állapot-visszacsatolást. Vegyük észre az algebrai hasonlóságot a folytonosidejű és diszkrétidejű feladat esetén. |
==5. Mik a fő problémák az egyszerű u=-Kx állapot-visszacsatolás esetén tipikus irányítási rendszerekben? == | ==5. Mik a fő problémák az egyszerű u=-Kx állapot-visszacsatolás esetén tipikus irányítási rendszerekben? == | ||
A lap 2014. február 6., 22:15-kori változata
Tartalomjegyzék
- 1 1. Milyen identifikációs rendszermodelleket ismer?
- 2 2. Miért van szükség identifikációra?
- 3 3. Mit értünk állapot-visszacsatolás alatt?
- 4 4. Mi lesz állapot-visszacsatolás esetén a zárt rendszer karakterisztikus egyenlete?
- 5 5. Mik a fő problémák az egyszerű u=-Kx állapot-visszacsatolás esetén tipikus irányítási rendszerekben?
- 6 6. Mi a domináns póluspár?
- 7 7. Mi a kapcsolat a kéttárolós lengő tag csillapítása és csillapítatlan sajátfrekvenciája valamint a hozzátartozó pólusok között?
- 8 8. Mi biztosítja a konstans alapjel követését állapot-visszacsatolt rendszerekben?
- 9 9. Miért szükséges állapotmegfigyelő alkalmazása?
- 10 10. Mi a kapcsolat a "terhelés" elnevezés és a zavaró jel között?
- 11 11. Hogyan küszöbölhető ki a terhelés hatása?
- 12 12. Mit értünk diszkrétidejű aktuális megfigyelő alatt és mik az előnyei?
- 13 13. Miért érdemes integrátort tenni a szabályozási körbe?
- 14 14. Hogyan képződik le egy folytonos idejű pólus a diszkrétidejű tartományba?
- 15 15. Mit okoznak a megfigyelő sajátértékei a zárt rendszer átviteli függvényében?
1. Milyen identifikációs rendszermodelleket ismer?
AR, ARX, IV, ARMAX stb. Ezek a modellek a MATLAB System Identification (röviden IDENT) toolboxa segítségével identifikálhatók. ARX modell a klasszikus LS (least squares) becsléssel is identifikálható. A módszerek érzékenyek a jel és zaj korreláltságára, amelyen segédváltozók (IV) alkalmazásával lehet javítani. Az ARMAX modell már általánosabb zajstruktúrát alkalmaz, de identifikációja numerikusan bonyolultabb módszert igényel, nevezetesen a kvázi Newton-módszert. Lásd elméleti alapok.
2. Miért van szükség identifikációra?
Az identifikáció célja dinamikus modell nyerése az ismeretlen rendszerről, a szabályozástechnikában a szabályozott szakaszról. Dinamikus modell hiányában csak kísérletezéssel tudnánk egyszerű szabályozók paraméterbeállítását megkeresni. A dinamikus modell ismerete lehetővé teszi elméletileg megalapozott szabályozások tervezését, amely minimálissá teszi a reális folyamaton való kísérletezést. A modell jó, ha azonos bemenő jel mellett a kimenetén hasonlóan válaszol, mint az ismeretlen rendszer. A modellel szemben pótlólagos elvárásaink is lehetnek, mint például az, hogy az identifikációval kapott diszkrétidejű modellnek legyen folytonosidejű megfelelője. Ez a negatív valós pólusokkal áll kapcsolatban a z-tartományban.
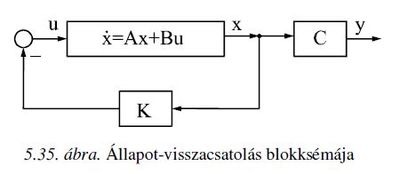
3. Mit értünk állapot-visszacsatolás alatt?
Állapot-visszacsatolás alatt azt értjük, hogy a szabályozó kimenő jelét (a beavatkozó jelet) az állapotokból állítjuk elő. Lineáris állapot-visszacsatolás esetén folytonos időben [math]u(t)=-K\cdot x(t)[/math], diszkrét időben pedig [math]u(iT)=-K\cdot x(it)[/math], vagy röviden [math]u_i=-K\cdot x_i[/math], ahol T a mintavételi idő. Egyváltozós (SISO) rendszer esetén K sorvektor.
4. Mi lesz állapot-visszacsatolás esetén a zárt rendszer karakterisztikus egyenlete?
Folytonos időben a szakasz állapotegyenlete [math]\dot{x}=Ax + Bu[/math], a zárt rendszer állapotegyenlete [math]\dot{x}=(A-BK) \cdot x[/math], a zárt rendszer karakterisztikus egyenlete pedig [math]\varphi_c(s)=det(sI-(A-BK))[/math]. Diszkrét időben a szakasz állapotegyenlete [math]x_{i+1}=\Phi \cdot x_i + \Gamma \cdot u_i[/math], a zárt rendszer állapotegyenlete [math]x_{i+1}=(\Phi-\Gamma K) \cdot x_i[/math], a zárt rendszer állapotegyenlete pedig [math]\varphi_c(z)=(zI-(\Phi - \GammaK))[/math]. A pólusáthelyezési feladatban előírjuk a zárt rendszer karakterisztikus egyenletét (ami ekvivalens a zárt rendszer pólusainak, azaz a velük megegyező sajátértékeknek az előírásával), és keressük az ehhez szükséges állapot-visszacsatolást. Vegyük észre az algebrai hasonlóságot a folytonosidejű és diszkrétidejű feladat esetén.