Záróvizsga kvíz - Algoritmusok

ZVAlgo

Kvízek használata, fejlesztése.
Statisztika
Átlagteljesítmény	-
Eddigi kérdések	0
Kapott pontok	0
Alapbeállított pontozás	(-)
-
Beállítások
Minden kérdés látszik	-
Véletlenszerű sorrend	-
-

Tekintsük az alábbi két függvényt (itt a log függvény kettes alapú logaritmust jelöl): (2023 jun)

[math]f(n)=2023 \cdot n^2 \cdot \log n-100 \cdot \sqrt{n}[/math]

[math]g(n)=\frac{1}{10^{10}} \cdot n^3+82 \cdot n \cdot \log n[/math]

Az alábbiak közül melyik állítás igaz?

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]f(n) \in O(g(n))[/math] , mert mindkét függvényre igaz, hogy [math]O\left(n^3\right)[/math]
2. [math]f(n) \in O(g(n))[/math] , mert [math]f(n) \in O\left(n^2\right)[/math] és [math]g(n) \in O\left(n^3\right)[/math]
3. [math]f(n) \in O(g(n))[/math] , de az előző két indoklás egyike sem helyes
4. [math]f(n) \notin O(g(n))[/math]

Egy bináris keresőfa preorder bejárása a csúcsokat [math]5, 2, 4, 12, 8, 7, 10, 20[/math] sorrendben látogatja meg. (2023 jun)

Melyik igaz az alábbi állítások közül a keresőfára?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. A 7 a 12 egyik részfájában van.
2. A 8 a gyökérben van.
3. A 10 a 2 egyik részfájában van.
4. A 2 egy levélbe n van.

[math]2n[/math] darab különböző csokiból hányféleképpen tudunk kiválasztani [math]n[/math] darabot úgy, hogy a három kedvenc csokink a kiválasztottak között legyen? (2023 jun)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]\left(\begin{array}{c}2 n \\ n\end{array}\right) \cdot\left(\begin{array}{l}n \\ 3\end{array}\right)[/math]
2. [math](2 n-3) \cdot(2 n-4) \cdot \ldots \cdot(n-2)[/math]
3. [math]\left(\begin{array}{c}2 n-3 \\ n\end{array}\right)[/math]
4. [math]\left(\begin{array}{c}2 n \\ n\end{array}\right) \cdot \frac{1}{3 !}[/math]

Radix rendezéssel rendezzük az alábbi sorozatot: [math]s_{1}=a b a c, s_{2}=a c b c, s_{3}=b c a c, s_{4}=b b b b, s_{5}=c a c b[/math] (a karakterek mindegyik pozícióban a 3-elemű [math]\{a, b, c\}[/math] ábécéből kerülnek ki). (2023 jun)

Melyik állítás igaz a rendezés folyamatára?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. [math]s_{5}=c a c b[/math] soha nem előzi meg az [math]s_{1}=a b a c[/math] szót.
2. Van olyan fázis, amikor [math] s_{3}=b c a c[/math] megelőzi az [math]s_{1}=a b a c[/math] szót.
3. [math]s_{3}=b c a c[/math] és [math]s_{4}=b b b b[/math] sorrendje pontosan kétszer változik.
4. Van olyan fázis, amikor [math]s_{3}=b c a c[/math] megelőzi az [math]s_{2}=a c b c[/math] szót.

Kruskal algoritmusát futtatjuk az alábbi gráfon. (2023 jun)

Hiba a bélyegkép létrehozásakor: Nem lehet a bélyegképet a célhelyre menteni

Melyik állítás igaz az alábbiak közül?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. Ha [math]x \le 3 [/math] akkor az [math]E C[/math] élet biztosan nem választja be az algoritmus a minimális feszítőfába.
2. Az [math]A C[/math] élet biztosan beválasztja az algoritmus a minimális feszítőfába, bármi is [math]x[/math] értéke.
3. Az [math]A C[/math] élet biztosan nem választja be az algoritmus a minimális feszítőfába, bármi is [math]x[/math] értéke.
4. Az algoritmus biztosan beválaszt legalább egy 3 súlyú élet a minimális feszítőfába.

Az [math]n[/math] csúcsú [math]G=(V, E)[/math] irányítatlan gráfra igaz, hogy bárhogyan is sorolunk fel [math]\left(v_{1}, v_{2}, \ldots, v_{k}\right)[/math] csupa különböző [math]G[/math] -beli csúcsokat, ahol [math]3 \leq k \leq n[/math] a [math]\left\{v_{1}, v_{2}\right\},\left\{v_{2}, v_{3}\right\}, \ldots,\left\{v_{k-1}, v_{k}\right\}[/math] és [math]\left\{v_{k}, v_{1}\right\}[/math] párok közül legalább az egyik benne van [math]G[/math] élhalmazában. Melyik állítás igaz az alábbiak közül? (2023 jun)

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. [math]G[/math] komplementerében nincsen kör.
2. [math]G[/math]-ben van kör.
3. [math]G[/math]-ben nincsen [math]k[/math] méretű független ponthalmaz.
4. [math]G[/math] komplementerében nincsen [math]k[/math] -as klikk.

Egy ország térképe egy élsúlyozott, irányítatlan [math]n[/math] csúcsú [math]G[/math] gráf szomszédossági mátrixával adott. A csomópontok a városok, az élek a városok között vezető közvetlen utak, egy él súlya a megfelelő útszakasz hosszát adja meg kilométerben. (2023 jun)

A városok közül néhányban van csak posta. Egy adott [math]k[/math] érték esetén azt szeretnénk eldönteni, hogy igaz-e, hogy bármelyik településről van [math]k[/math] kilométeren belül elérhető, postával rendelkező város (az eléréshez csak az úthálózatot használhatjuk). Az alábbi lehetőségek közül melyikkel lehet ezt eldönteni [math]O\left(n^{2}\right)[/math] lépésben?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. Felveszünk egy új csúcsot, ebből 0 súlyú élet vezetünk minden postás városhoz, majd szélességi bejárást (BFS) futtatunk az új csúcsból a legrövidebb utak megkeresésére.
2. Minden csúcsból futtatunk egy szélességi bejárást (BFS) a legrövidebb utak megkeresésésére.
3. Minden csúcsból lefuttatjuk Dijktsra algoritmusát a legrövidebb utak megkeresésére.
4. Felveszünk egy új csúcsot, ebből 0 súlyú élet vezetünk minden postás városhoz, majd futtatjuk Dijkstra algoritmusát az új csúcsból a legrövidebb utak megkeresésére.

Eldöntési feladatok (2023 jun)

Az [math]X_{1}[/math] eldöntési feladatban egy irányítatlan [math]G[/math] gráfról azt szeretnénk eldönteni, hogy van-e [math]G[/math] -ben pontosan 4 élü kör. Az [math]X_{2}[/math] eldöntési feladatban egy irányítatlan [math]G[/math] gráfról és egy pozitív egész [math]k[/math] számról azt szeretnénk eldönteni, hogy van-e [math]G[/math] -ben pontosan [math]k[/math] élü kör. Melyik állítás igaz az alábbiak közül, ha feltesszük, hogy [math]P \neq N P[/math] ?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. [math]X_{1} \in P[/math] és [math]X_{2} \in N P \backslash P \checkmark[/math]
2. [math]X_{1} \in P[/math] és [math]X_{2} \in P[/math]
3. [math]X_{1} \in \operatorname{coN} P[/math] de [math]X_{1} \notin P[/math]
4. [math]X_{1} \in P[/math] de [math]X_{1} \notin N P[/math]

Az [math]X[/math] eldöntési problémáról azt tudjuk, hogy [math]N P[/math] -ben van, az [math]Y[/math] eldöntési problémáról pedig azt, hogy [math]N P[/math] -teljes. (2023 jun)

Mi igaz az alábbiak közül, ha feltételezzük, hogy [math]P \neq N P[/math] ?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. Minden olyan eldöntési probléma, ami Karp-redukálható [math]Y[/math] -ra, az Karp-redukálható [math]X[/math] -re is.
2. [math]Y[/math] biztosan Karp-redukálható [math]X[/math] -re. [math]{ }^{X}[/math]
3. Ha [math]X[/math] Karp-redukálható [math]Y[/math] -ra, akkor [math]X[/math] nincsen [math]P[/math] -ben.
4. Ha [math]Y[/math] Karp-redukálható [math]X[/math] -re, akkor az [math]X[/math] probléma [math]N P[/math] -teljes.

Adott egy egész számokat tartalmazó [math]A[1: n][/math] tömb, melyben nem szerepel 0. (2023 jun)

Az [math]A[1: n][/math] tömb alapján egy [math]P[1: n][/math] és egy [math]N[1: n][/math] tömböt töltünk ki a következőképpen:

• ha [math]A[1]\gt 0[/math] akkor [math]P[1]=A[1][/math] és [math]N[1]=A[1][/math] .
• ha [math]A[1] \le 0 [/math] akkor [math]P[1]=0[/math] és [math]N[1]=A[1][/math]

A további értékeket [math](i\gt 2)[/math] így számoljuk:

• ha [math]A[i]\gt 0[/math] akkor [math]P[i]=P[i-1]+A[i][/math] és [math]N[i]=\max \{N[i-1]+A[i], A[i]\}[/math]
• ha [math]A[i] \le 0[/math] akkor [math]P[i]=0[/math] és [math]N[i]=P[i-1]+A[i][/math]

Melyik állítás igaz az alábbiak közül a kiszámolt [math]P[i][/math] és [math]N[i][/math] értékek jelentésére?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. [math]N[i][/math] megadja a legnagyobb összeget, amit valamelyik, legfeljebb egy negatív számot tartalmazó [math]A[j: i][/math] résztömbből ( [math]1 \leq j \leq i)[/math] kaphatunk úgy, ha a résztömb minden elemét összeadjuk.
2. [math]P[i][/math] megadja a legnagyobb összeget, amit valamelyik [math]A[j: i][/math] résztömbből [math](1 \leq j \leq i)[/math] kaphatunk úgy, ha a résztömb minden elemét összeadjuk.
3. [math]N[i][/math] megadja az [math]A[1: i][/math] tömbben szereplö összes negatív szám összegét
4. [math]P[i][/math] megadja az [math]A[1: i][/math] tömbben szereplö összes szám összegét

Egy irányítatlan nyolc csúcsú gráfon BFS-t (szélességi bejárást) futtatunk úgy, hogy ha döntési helyzetben vagyunk, akkor az ábécé szerinti sorrend szerint haladunk. A BFS fába az alábbi élek kerülnek be ebben a sorrendben: [math]AB, AC, AD, CE, DF, EH, FG[/math]. (2023 jan)

Melyik csúcs lehet szomszédja az [math]F[/math] csúcsnak a gráfban?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. A
2. B
3. C
4. E

Tekintsük az alábbi három függvényt (itt a log függvény kettes alapú logaritmust jelöl): (2023 jan)

[math]f(n)=n !+10 \cdot n^{2}-3[/math]

[math]g(n)=\frac{1}{8} n^{n}+9 \cdot \log n[/math]

[math]h(n)=10^{1000} \cdot n^{1000}+37 \cdot n^{3}+42[/math]

Az alábbiak közül melyik állitás igaz ezen három függvény nagyságrendjére?

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. [math]f(n) \in O(g(n)) \text { és } g(n) \in O(h(n))[/math]
2. [math]f(n) \in O(g(n)) \text { és } g(n) \notin O(h(n))[/math]
3. [math]f(n) \notin O(g(n)) \text { és } g(n) \in O(h(n))[/math]
4. [math]f(n) \notin O(g(n)) \text { és } g(n) \notin O(h(n))[/math]

Az alábbi lehetőségek közül melyik az a változtatás, amit ha végrehajtunk a 10,5,7,6,2, 3 számsorozaton, akkor van olyan bináris keresőfa, amiben egy keresés során láthatjuk a kapott új sorozat elemeit ebben a sorrendben? (2023 jan)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. 2 helyett álljon 4
2. 7 helyett álljon 8
3. 5 helyett álljon 1
4. 10 helyett álljon 1

Egy [math]k[/math] és egy [math]\ell[/math] hosszú rendezett tömböt fésülünk össze a tanult összefésülés eljárással. Maximum mennyi összehasonlítás történhet eközben? (2023 jan)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]k \cdot \ell[/math]
2. [math]k+\ell-1[/math]
3. [math]\max \{k, \ell\}[/math]
4. [math]k+\ell x[/math]

Egy csupa különböző egész számot tartalmazó [math]T[/math] tömbben akarjuk eldönteni egy adott [math]x[/math] elemről, hogy igaz-e, hogy [math]x[/math] és [math]2 \cdot x[/math] is szerepel [math]T[/math]-ben. Az alábbi négy állítás közül melyek igazak? (2023 jan)

A: Ez megtehető [math]O(n)[/math] lépésben, ha a tömb rendezett.

B: Ez megtehető [math]O(\log n)[/math] lépésben, ha a tömb rendezett.

C: Ez megtehető [math]O(n)[/math] lépésben tetszőleges tömb esetén.

D: Ez megtehető [math]O(\log n)[/math] lépésben tetszőleges tömb esetén.

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. Csak az [math]A, B[/math] állítások igazak.
2. Csak az [math]A, B, C[/math] állítások igazak.
3. Mind a négy igaz.
4. Csak az [math]A, C[/math] állítások igazak.

Egy országban a rendszámok hét karakterből állnak, az első négy karakter egy 26 elemú ábécéből kerül ki, az utolsó három karakter pedig a [math]0,1,2,3,4,5,6,7,8,9[/math] halmazból. További megkötés nincs a rendszámokra. (2023 jan)

Hány olyan rendszám van, ahol az első két betû megegyezik és a három számjegyből a középső a 0 ?

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. [math]3 \cdot 26+2 \cdot 10[/math]
2. [math]26^{3} \cdot 10^{2}[/math]
3. [math]26^{3}+10^{2}[/math]
4. [math]3 \cdot 2 \cdot 26 \cdot 10[/math]

Adott egy 200 elemű [math]T[1: 200][/math] tömb, amiben [math]T[3 i]=i[/math] minden [math]1 \leq i \leq 66[/math] esetén, minden egyéb esetben (azaz amikor az index nem többszöröse a 3-nak) pedig [math]T[j]=-1[/math]. (2023 jan)

Definiáljuk az [math]A[/math] tömböt a következőképpen: [math]A[1]=T[1][/math]

és [math]1 \le j \leq 200[/math] esetén [math]A[j]=\max \{A[j-1]+T[j], T[j]\}[/math].

Mennyi [math]A[4][/math] értéke?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. 1
2. [math]-1[/math]
3. [math]-2[/math]
4. 0

Az előző feladat folytatása: Mi igaz az alábbiak közül a kitöltött [math]A[1: 200][/math] tömb elemeire?

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]A[j]=A[j-1][/math] teljesül legalább 50 esetben
2. [math]A[j]=T[j][/math] teljesül legalább 50 esetben
3. [math]A[j]\gt 0[/math] teljesül legalább 50 esetben [math]\checkmark[/math]
4. [math]A[200][/math] a legnagyobb érték az [math]A[1: 200][/math] tömbben.

Egy ország térképe egy élsúlyozott, irányítatlan [math]G[/math] gráf szomszédossági mátrixával adott. A csomópontok a városok, az élek a városok között vezető közvetlen utak, az élek súlya pedig azt adja meg, hogy az autónk az adott útszakaszon hány liter benzint fogyaszt. (2023 jan)

Adott egy [math]A[/math] csomópont, ahol éppen tartózkodunk és tudjuk hogy [math]B[/math] liter benzinünk van. Melyik tanult algoritmussal lehet meghatározni, hogy az ország mely városaiba tudunk eljutni tankolás nélkül?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. BFS-t, azaz szélességi bejárást kell futtatni az [math]A[/math] csúcsból.
2. Kruskal algoritmust kell futtatni a gráfon.
3. DFS-t, azaz mélységi bejárást kell futtatni az [math]A[/math] csúcsból.
4. Dijkstra algoritmust kell futtatni az [math]A[/math] csúcsból.

Legyen [math]X[/math] az az eldöntési probléma, melynek inputja egy irányított [math]G[/math] gráfból, ezen gráf egy [math]s[/math] csúcsából és egy [math]k[/math] pozitív egészből áll és azt szeretnénk eldönteni, hogy igaz-e hogy [math]G[/math]-ben [math]s[/math]-ből minden más csúcsba vezet legfeljebb [math]k[/math] élből álló út. Legyen továbbá [math]Y[/math] a tanult [math]3-S Z[/math] IíN eldöntési feladat. (2023 jan)

Mi igaz az alábbiak közül, ha feltételezzük, hogy [math]P \neq N P[/math] ?

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. [math]X[/math] sem Karp-redukálható [math]Y[/math]-ra és [math]Y[/math] sem Karp-redukálható [math]X[/math]-re.
2. [math]X[/math] Karp-redukálható [math]Y[/math]-ra, de [math]Y[/math] nem Karp-redukálható [math]X[/math]-re.
3. [math]X[/math] Karp-redukálható [math]Y[/math]-ra és [math]Y[/math] is Karp-redukálható [math]X[/math]-re.
4. [math]X[/math] nem Karp-redukálható [math]Y[/math]-ra, de [math]Y[/math] Karp-redukálható [math]X[/math]-re. [math]X[/math]

Tekintsük azt az eldöntési feladatot, ahol egy irányítatlan [math]G[/math] gráfról azt szeretnénk eldönteni, hogy hozzá lehet-e adni legfeljebb 5 élet [math]G[/math]-hez úgy, hogy a keletkező gráfban legyen 100 pontú teljes részgráf. (Új csúcsot nem adunk hozzá a gráfhoz, csak éleket húzunk be a már meglevő csúcsok közé.) (2023 jan)

Melyik állítás igaz az alábbiak közül, ha feltesszük, hogy [math]P \neq N P[/math] ?

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. A probléma [math]P[/math]-ben van, de nincs [math]NP[/math]-ben.
2. A probléma [math]NP[/math]-teljes és nincs [math]P[/math]-ben.
3. A probléma [math]P[/math]-ben van és [math]N P[/math]-teljes.
4. A probléma [math]P[/math]-ben és [math]N P[/math]-ben is benne van.

Pozitív egész számokat szeretnénk tárolni valami adatszerkezet segítségével úgy, hogy [math]n[/math] tárolt elem esetén tetszőleges [math]x[/math] egész számról [math]O(\log n)[/math] lépésben meg tudjuk mondani, hogy igaz-e rá, hogy [math]x[/math] a tárolt számok között van, de sem [math]x-1[/math] , sem [math]x+1[/math] nincsen. (2022 jun)

Melyik adatszerkezettel valósítható ez meg?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. 2-3 fa
2. rendezett lista
3. nyílt címzésú hash
4. (nem feltétlenül kiegyensúlyozott) bináris keresőfa

Az 1, 8, 10,12, 20, 27, 30 rendezett tömbben bináris kereséssel keressük a 30-at. Hány összehasonlítás után találjuk meg? (2022 jun)

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. 2
2. 1
3. 7
4. 3

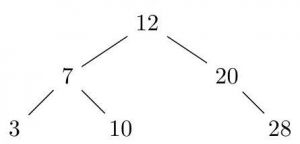
Egy kezdetben üres bináris keresőfába szúrtunk be elemeket (törlés nem volt). Az alábbiak közül melyik beszúrási sorrend eredményezi az ábrán látható fát? (2022 jun)

Hiba a bélyegkép létrehozásakor: Nem lehet a bélyegképet a célhelyre menteni

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]5,9,1,7,3,4[/math]
2. [math]5,7,4,9,3,1[/math]
3. [math]5,3,4,9,1,7[/math]
4. [math]5,4,7,3,9,1[/math]

Tekintsük azt a feladatot, ahol egy [math]n\gt 100[/math] csúcsú irányított [math]G[/math] gráfról azt szeretnénk eldönteni, hogy van-e 100 olyan csúcsa, hogy a gráfból ezeket elhagyva a maradék gráf csupa izolált pontból áll. (2022 jun)

Melyik állítás igaz az alábbiak közül, ha feltesszük, hogy [math]P \neq N P[/math] ?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. A probléma [math]P[/math] -ben van, de nincs [math]N P[/math] -ben.
2. A probléma [math]N P[/math] -teljes és nincs [math]P[/math] -ben.
3. A probléma [math]P[/math] -ben van és [math]N P[/math] -teljes.
4. A probléma [math]P[/math] -ben és [math]N P[/math] -ben is benne van.

A megadottak közül melyik egy topologikus sorrendje az ábrán látható gráfnak? (2022 jun)

Hiba a bélyegkép létrehozásakor: Nem lehet a bélyegképet a célhelyre menteni

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. [math]A, B, D, E, F, G, H, C[/math]
2. [math]A, D, F, G, H, C, E, B[/math]
3. [math]A, B, C, D, E, F, G, H[/math]
4. [math]A, D, F, E, B, G, H, C[/math]

Egy [math]n \times n[/math] -es táblázat mezőin akarunk eljutni a bal felső cellából az utolsó sorba (itt mindegy, hogy a soron belül melyik oszlopba érkezünk). (2022 jun)

A szabályok a következők:

1. Az első oszlop első mezőjéről kell indulnunk és a végén az utolsó sor tetszőleges mezőjére kell érkeznünk.
2. Egy lépésben vagy egy cellát mehetünk lefele (és maradunk ugyanabban az oszlopban) vagy egy cellát megyünk jobbra (és maradunk ugyanabban a sorban) vagy átlósan lépünk egyet lefele jobbra (azaz egy sort lefele és egy oszlopnyit jobbra).

Jelölje [math]T[i, j](1 \leq i, j \leq n[/math] esetén) azt, hogy az [math]i[/math] -edik sor [math]j[/math] -edik oszlopában levő mezőbe hányféleképpen juthatok el a bal felső cellából. Inicializáljuk a kezdeti értékeket így: mivel az első sor minden cellájába egyféleképpen juthatunk, ezért [math]T[1, j]=1[/math] minden [math]1 \leq j \leq n[/math] esetén és hasonlóan, mivel az első oszlop minden cellájába is egy út vezet, ezért [math]T[i, 1]=1[/math] minden [math]1 \leq i \leq n[/math] esetén. Melyik rekurziós képlet a helyes a többi [math]T[i, j][/math] érték meghatározására?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. [math]T[i, j]=T[i-1, j]+T[i, j-1]+T[i-1, j-1][/math]
2. [math]T[i, j]=\max \{T[i-1, j], T[i, j-1], T[i-1, j-1]\}[/math]
3. [math]T[i, j]=T[i-1, j]+T[i, j-1]+T[i-1, j-1]+1[/math]
4. [math]T[i, j]=T[i-1, j-1]+1[/math]

Az előző feladat folytatása:

A teljesen kitöltött [math]T[/math] táblázat segítségével hogyan kaphatjuk meg azt, hogy hányféleképpen lehet eljutni a bal felső cellából a legalsó sorba?

Típus: egy. Válasz: 5. Pontozás: nincs megadva.

1. [math]\max _{1 \le i \le n} T[i, n][/math] adja meg ezt.
2. [math]\Sigma_{i=1}^{n} T[i, n][/math] adja meg ezt.
3. [math]T[n, n][/math] adja meg ezt.
4. [math]\max _{1 \leq j \leq n} T[n, j][/math] adja meg ezt
5. [math]\Sigma_{j=1}^{n} T[n, j][/math] adja meg ezt.

A [math]G[/math] egyszerű, irányítatlan gráf élei súlyozottak. Tegyük fel, hogy az élek súlyai különbözőek és hogy van legalább három éle a gráfnak. (2022 jun)

Tekintsük a következő állításokat: A: [math]G[/math] minden minimális feszítőfája tartalmazza a legkisebb súlyú élt. B: [math]G[/math] minden minimális feszítőfája tartalmazza a második legkisebb súlyú élt. C: [math]G[/math] egyik minimális feszítőfája sem tartalmazza a legnagyobb súlyú élt. Melyik a helyes az alábbi lehetőségek közül?

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. Csak az [math]A[/math] állítás igaz, a másik kettő nem
2. Az [math]A[/math] , a [math]B[/math] és a [math]C[/math] állítás is igaz.
3. Csak az [math]A[/math] és a [math]B[/math] állítás igaz, a [math]C[/math] nem.
4. Csak az [math]A[/math] és a [math]C[/math] állítás igaz, a [math]B[/math] nem.

Legyen [math]X[/math] a [math]2SZÍN[/math] eldöntési probléma, azaz ahol egy egyszerü, irányítatlan [math]G[/math] gráfról azt szeretnénk eldönteni, hogy ki lehet-e színezni a csúcsait két színnel úgy, hogy azonos színú csúcsok közőtt ne menjen él. Az [math]Y[/math] eldöntési problémában pedig azt kell eldöntenünk [math]n[/math] darab pozitív egész számról, hogy van-e ezeknek a számoknak egy olyan részhalmaza, hogy a részhalmazban levő számok összege megegyezik a részhalmazba be nem vett számok összegével. (2022 jun)

Mi igaz az alábbiak közül, ha feltételezzük, hogy [math]P \neq N P[/math] ?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. [math]X[/math] nem Karp-redukálható [math]Y[/math] -ra, de [math]Y[/math] Karp-redukálható [math]X[/math] -re.
2. [math]X[/math] Karp-redukálható [math]Y[/math] -ra és [math]Y[/math] is Karp-redukálható [math]X[/math] -re.
3. [math]X[/math] sem Karp-redukálható [math]Y[/math] -ra és [math]Y[/math] sem Karp-redukálható [math]X[/math] -re.
4. [math]X[/math] Karp-redukálható [math]Y[/math] -ra, de [math]Y[/math] nem Karp-redukálható [math]X[/math] -re.

Tekintsük azt a [math]K_{20,40}[/math] teljes páros gráfot, melynek [math]A=\left\{a_{1}, a_{2}, \ldots, a_{20}\right\}[/math] és [math]B=\left\{b_{1}, b_{2}, \ldots, b_{40}\right\}[/math] a két osztálya. Hány maximális (azaz tovább nem bővíthető) párosítás van ebben a gráfban? (Két párosítás különböző, ha nem pontosan ugyanazokból az [math]\left(a_{i}, b_{j}\right)[/math] élekből áll.) (2022 jun)

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. [math]\left(\begin{array}{l}40 \\ 20\end{array}\right) \cdot 20[/math] !
2. [math]\left(\begin{array}{l}40 \\ 20\end{array}\right)[/math]
3. [math]40^{20}[/math]
4. [math]40![/math]

Az [math]1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16[/math] tömböt rendezzük a szokásos (módosítás nélkül futtatott) öszefésüléses rendezéssel. Hány összehasonlítás történik a rendezés teljes futása alatt? (2022 jun)

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. 0
2. 64
3. [math]\left(\begin{array}{c}16 \\ 2\end{array}\right)[/math]
4. 32

Az [math]\mathcal{A}[/math] algoritmusról tudjuk, hogy lépésszáma a bemenet hosszának, [math]n[/math] -nek a függvényében [math]O\left(n^{2}\right)[/math] . (2022 jun)

Melyik nem igaz az alábbiak közül?

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. Minden [math]n[/math] pozitív számhoz lehet olyan [math]n[/math] hosszú bemenet, amelyiken [math]\mathcal{A}[/math] lépésszáma kisebb, mint [math]n^{3}[/math] .
2. Minden [math]n[/math] pozitív számhoz lehet olyan [math]n[/math] hosszú bemenet, amelyiken [math]\mathcal{A}[/math] lépésszáma nagyobb, mint [math]n^{3}[/math] .
3. Minden [math]n[/math] pozitív számhoz lehet olyan [math]n[/math] hosszú bemenet, amelyiken [math]\mathcal{A}[/math] lépésszáma kisebb, mint [math]n[/math] .
4. Minden [math]n[/math] pozitív számhoz lehet olyan [math]n[/math] hosszú bemenet, amelyiken [math]\mathcal{A}[/math] lépésszáma nagyobb, mint [math]n[/math] .

Egy csupa különböző egész számot tartalmazó bináris keresőfában egy keresés során az alábbi értékeket látjuk (x értéke nem ismert): [math]10, 5, x, 7, 8[/math] . Az alábbiak közül mi igaz x értékére? (2022 jan)

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. x lehet 1 is és 9 is
2. x lehet 6 is és 9 is
3. x lehet 1 is és 6 is
4. x lehet 2 is és 12 is

Egy kezdetben üres bináris keresőfába beszúrtuk az egész számokat valamilyen sorrendben (a sorrend nem ismert). Mi igaz biztosan az alábbiak közül? (2022 jan)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. Az 1 levélben van.
2. A fának 7 szintje van.
3. A legutoljára beszúrt érték levélben van.
4. A középső érték, azaz a 64, a gyökérben van.

Egy irányítatlan nyolc csúcsú gráfon DFS-t (mélységi bejárást) futtatunk úgy, hogy ha döntési helyzetben vagyunk, akkor az ábécé szerinti sorrend szerint haladunk. A DFS fába az alábbi élek kerülnek be ebben a sorrendben: [math]AB, BD, AF, FE, EC, FG, GH[/math] . Mi igaz a csúcs fokszámára az alábbiak közül? (2022 jan)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]H[/math] fokszáma lehet 1 vagy 2, és más nem lehet
2. [math]H[/math] fokszáma lehet 1, 2, 3 vagy 4, és más nem lehet
3. [math]H[/math] fokszáma lehet 1, 2 vagy 3, és más nem lehet
4. [math]H[/math] fokszáma lehet 1, 2, 3, 4 vagy 5, és más nem lehet

Adott egy [math]3n[/math] csúcsú teljes gráf, a csúcsok számozottak, az 1, 2,…, n számozású csúcsok pirosra vannak színezve, a többi csúcs színtelen. Hány olyan különböző Hamilton-út van a gráfban, amelyben az első n csúcs piros? (2022 jan)

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. [math]\frac{n!}{2} * n![/math]
2. [math]n! * n! * n![/math]
3. [math]2 * n! * n![/math]
4. [math]n! * (2n)![/math]

A [math]4, 3, 2, 1, 5, 6, 7, 8[/math] tömböt rendezzük öszefésüléses rendezéssel. Hány összehasonlítás történik a rendezés teljes futása alatt? (2022 jan)

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. 12
2. 7
3. 4
4. 8

Radix rendezéssel rendezünk 5 hosszú karaktersorozatokat, ahol a karakterek mindegyik pozícióban a 4-elemű [math]\{a,b,c,d\}[/math] ábécéből kerülnek ki. Mi igaz ekkor a radix rendezés során használt ládarendezésekre? (2022 jan)

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. 1 ládarendezést használunk [math]4^5[/math] ládával.
2. 5 ládarendezést használunk, mindegyik esetben 4 ládával.
3. 4 ládarendezést használunk, mindegyik esetben 5 ládával.
4. 1 ládarendezést használunk 20 ládával.

Tekintsük az alábbi három függvényt (itt a [math]log[/math] függvény mindig kettes alapú logaritmust jelöl): (2022 jan)

[math]f(n)=2022 \cdot n^2 \cdot \log n+7 \cdot \sqrt{n}[/math]

[math]g(n)=\log n+1000+n \cdot(\log n)^2[/math]

[math]h(n)=n \cdot \sqrt{n}+\frac{1}{1000} \cdot n^2-8[/math]

Az alábbiak közül melyik állítás igaz ezen három függvény nagyságrendjére?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. [math]f(n) \notin O(h(n))[/math] és [math]g(n) \in O(h(n))[/math]
2. [math]f(n) \in O(h(n))[/math] és [math]g(n) \notin O(h(n))[/math]
3. [math]f(n) \in O(h(n))[/math] és [math]g(n) \in O(h(n))[/math]
4. [math]f(n) \notin O(h(n))[/math] és [math]g(n) \notin O(h(n))[/math]

Tekintsük azt az eldöntési feladatot, ahol egy irányított [math]G[/math] gráfról azt szeretnénk eldönteni, hogy van-e két olyan [math]s[/math] és [math]t[/math] csúcsa, hogy [math]s[/math] -ből van irányított út [math]t[/math] -be, de [math]t[/math] -ből nincsen irányított út [math]s[/math] -be (2022 jan)

Melyik állítás igaz az alábbiak közül, ha feltesszük, hogy [math]P \neq NP[/math] ?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. A probléma [math]P[/math] -ben és [math]NP[/math] -ben is benne van.
2. A probléma [math]P[/math] -ben van, de nincs [math]NP[/math] -ben.
3. A probléma [math]NP[/math] -teljes és nincs [math]P[/math] -ben.
4. A probléma [math]P[/math] -ben van és [math]NP[/math] -teljes.

Legyen [math]X[/math] az az eldöntési probléma, ahol egy irányítatlan [math]G[/math] páros gráfról és egy [math]k[/math] számról azt szeretnénk eldönteni, hogy van-e [math]G[/math] -ben [math]k[/math] élű párosítás és legyen [math]Y[/math] az a kérdés, ahol egy irányítatlan [math]G[/math] gráfról és egy számról azt szeretnénk eldönteni, hogy van-e [math]G[/math] -ben [math]k[/math] pontból álló klikk (azaz teljes gráf). (2022 jan)

Mi igaz az alábbiak közül, ha feltételezzük, hogy [math]P \neq NP[/math] ?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. [math]X[/math] Karp-redukálható [math]Y[/math] -ra, de [math]Y[/math] nem Karp-redukálható [math]X[/math] -re.
2. [math]X[/math] nem Karp-redukálható [math]Y[/math] -ra, de [math]Y[/math] Karp-redukálható [math]X[/math] -re.
3. [math]X[/math] Karp-redukálható [math]Y[/math] -ra és [math]Y[/math] is Karp-redukálható [math]X[/math] -re.
4. [math]X[/math] sem Karp-redukálható [math]Y[/math] -ra és [math]Y[/math] sem Karp-redukálható [math]X[/math] -re.

A hátizsák feladatra tanult dinamikus programozást használó algoritmust futtatjuk [math]C = 10[/math] -es hátizsák kapacitással. A táblázat [math]i = 7[/math] -es sora az értékekkel így néz ki: (2022 jan)

X	0	1	2	3	4	5	6	7	8	9	10
7	0	0	7	7	8	12	12	12	12	20	20

Mi igaz a következő, [math]i = 8[/math] -as sor [math]V[8,b][/math] értékeire az alábbiak közül, ha a 8. tárgy [math]w_8[/math] súlya [math]5[/math] , [math]v_8[/math] értéke pedig [math]6[/math] ? ( [math]V[i,b][/math] jelentése: az első [math]i[/math] tárgyból [math]b[/math] hátizsák kapacitás mellett elérhető maximális érték.)

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. [math]V[8,4]=8 \text { és } V[8,9]=17[/math]
2. [math]V[8,3]=7 \text { és } V[8,8]=13[/math]
3. [math]V[8,4]=8 \text { és } V[8,8]=12[/math]
4. [math]V[8,4]=5 \text { és } V[8,8]=12[/math]

Az alábbi állítások közül pontosan egy hamis. Válassza ki a HAMIS állítást! (2021 jan)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. Előfordulhat, hogy egy bináris keresőfában végrehajtott keresés belső csúcsban (azaz nem levélben) ér véget.
2. Bináris keresőfában a legkisebb értéket tartalmazó csúcsnak legfeljebb egy gyereke lehet.
3. Bináris keresőfában a tárolt értékek közül a középsőt 1 lépésben meg lehet találni, mert az mindig a gyökérben van.
4. Piros-fekete fában a legkisebb értéket tartalmazó csúcsnak legfeljebb egy gyereke lehet.

Legyen [math]G(V, E)[/math] egy egyszerú, irányítatlan gráf. Tekintsük a következő tulajdonságot: (2021 jan)

Vannak olyan [math]X \subseteq V[/math] és [math]Y \subseteq V[/math] nemüres halmazok, melyekre igaz, hogy

• [math]X \cap Y=\emptyset[/math]
• [math]X \cup Y=V[/math]
• bármely [math]\{u, v\} \in E[/math] él esetén az [math]\{u, v\} \cap X[/math] halmaz egy elemú.

Az alábbiak közül melyik írja le pontosan a megadott tulajdonságú gráfokat?

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. Nincsen egyetlen éle sem a gráfnak.
2. A gráf páros gráf, de nem feltétlenül teljes páros gráf
3. A gráf teljes páros gráf
4. A gráf teljes gráf.
5. A gráfban van teljes párosítás

Az alábbi bináris keresőfa csúcsait a posztorder és a preorder bejárás szerinti sorrendben is kiírjuk. (2021 jan)

Hiba a bélyegkép létrehozásakor: Nem lehet a bélyegképet a célhelyre menteni

Melyik álítás igaz?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. A 3 előbb jön, mint a 27 mindkét sorrendben.
2. A 15 megelőzi a 4-et a preorder sorrendben, mert a 15 belső csúcsban van, a 4 pedig levélben.
3. A 27 megelőzi a 9-et a posztorder sorrendben, mert a 27 levélben van, a 9 pedig belső csúcsban.
4. A számok növekvő sorrendben vannak a két sorrend egyike szerint.
5. A 3 után közvetlenül a 4 következik a két sorrend valamelyikében.

Melyik állítás igaz az alábbi négy függvény nagyságrendjére? (2021 jan)

(a) [math]100 \cdot \frac{n(n-1)}{n-2} \cdot \log _{2} n+17 n-32[/math]

(b) [math]2 \cdot n^{2} \cdot \sqrt{n}+44 n^{2}+13[/math]

(c) [math]\frac{1}{10^{10}} \cdot \frac{4^{n}}{2^{n}}[/math]

(d) [math]4 n^{2}+37 n-12[/math]

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. Az (a) függvény [math]O\left(2^{n}\right)[/math], a (b) függvény [math]O\left(n^{2}\right)[/math]
2. [math]\mathrm{Az}[/math] (a) és a (d) függvény is [math]O\left(n^{2}\right)[/math]
3. [math]\mathrm{Az}[/math] (b) függvény [math]O\left(n^{n}\right)[/math], a (c) függvény [math]O\left(n^{2}\right)[/math]
4. A négy függvény közül csak a (d) függvény [math]O\left(n^{2}\right)[/math]
5. A (b), a (c) és a (d) függvény is [math]O\left(n^{2}\right)[/math]

Legyen [math]X[/math] egy [math]n[/math] elemú véges halmaz, [math]n\gt 0[/math]. Hány páratlan elemú részhalmaza van [math]X[/math]-nek? (2021 jan)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]n[/math]
2. [math]2^{\lfloor n / 2\rfloor}[/math]
3. [math]2^{n-1}[/math]
4. [math]2^{n}[/math]
5. Más a formula attól függően, hogy [math]n[/math] páros vagy páratlan.

Egy város úthálózatát a [math]G[/math] egyszerú, irányítatlan, összefüggő gráf írja le, a gráf csúcsai a csomópontok, az élek az ezeket összekötőútszakaszokat jelölik. (2021 jan)

Az utak sajnos eléggé rossz állapotúak, minden élre adott, hogy azt az útszakaszt mennyiért lehetne felújítani. A város vezetése azt szeretné megtudni, hogy mely útszakaszokat újitassa fel, ha a célja az, hogy a [math]v[/math] csúccsal jelzett főtérről mindencsomópontba el lehessen jutni kizárólag felújított útszakaszokon. A következő ötletek merültek fel a legolcsóbb ilyen felújitás megtalálására: A: Dijkstra algoritmusával határozzák meg a legrövidebb utakat [math]v[/math]-ből az összes többi csúcsba. B: A Bellman-Ford-algoritmussal határozzák meg a legrövidebb utakat [math]v[/math]-ből az összes többi csúcsba. C: Kruskal algoritmusával határozzanak meg egy minimális feszítófát a gráfban. Melyik ad helyes eredményt a feladatra?

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. Csak az A módszer.
2. Csak a B módszer.
3. Csak a C módszer
4. Csak az A és a B módszer.
5. Mindhárom módszer

Tudjuk, hogy az [math]\mathcal{A}[/math] probléma [math]N P[/math]-teljes, a [math]\mathcal{B}[/math] probléma pedig [math]N P[/math]-beli, de nem feltétlenül [math]N P[/math]-teljes. (2021 jan)

Tekintsük a következő álításokat:

A: Ha az [math]\mathcal{A}[/math] problémára van polinom idejü algoritmus, akkor [math]P=N P[/math].

B: Ha a [math]\mathcal{B}[/math] problémára van polinom idejú algoritmus, akkor [math]P=N P[/math].

C: Ha az [math]\mathcal{A}[/math] problémára van polinom idejú algoritmus, akkor a [math]\mathcal{B}[/math] problémára is van polinom idejú algoritmus.

Melyik helyes az alábbiak közül?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. Csak az A és a C igaz.
2. Csak az A igaz.
3. Az A, B, C mindegyike igaz.
4. Csak a B igaz.
5. Csak az A és a B igaz.

Adott egy [math]n[/math] hosszú számsorozat, [math]a_{1}, a_{2}, \ldots, a_{n}[/math]. (2021 jan)

Definiáljuk a [math]T[/math] és [math]S[/math] tömböt a következőképpen:

[math]T[0]=S[0]=0, T[1]=a_{1}[/math]

és [math]1 \le i \leq n[/math] esetén:

[math]T[i]=\max _{j \le i-1}\left\{T[j]+a_{i}\right\}[/math]

[math]S[i]=\max _{j \leq i}\{T[j]\}[/math]

Legyen most a számsorozat olyan, hogy ha [math]i[/math] hárommal osztható, akkor [math]a_{i}=3[/math], különben meg [math]a_{i}=1[/math].

Az alábbiak közül melyik állítás helyes?

Típus: egy. Válasz: 5. Pontozás: nincs megadva.

1. [math]T[10]=10[/math]
2. [math]T[4]=4[/math]
3. [math]S[10]=9[/math]
4. [math]S[3 n]=3 n[/math]
5. [math]T[36]=37[/math]

Adott [math]n[/math] tárgy, tudjuk, hogy az [math]i[/math]-ediknek a súlya [math]s_{i}[/math] kilogramm, az értéke [math]v_{i}[/math] forint, az [math]s_{i}, v_{i}[/math] számok pozitív egészek. (2021 jan)

Azt szeretnénk eldönteni, hogy ki lehet-e közülük választani néhányat úgy, hogy ezek berakhatók legyenek egy összesen 100 kg teherbírású zsákba, és a kiválasztott tárgyak értékeinek összege legalább 2021 Ft legyen. Melyik állítás igaz az alábbiak közül, ha feltesszük, hogy [math]P \neq N P[/math]?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. A probléma [math]P[/math]-ben és [math]N P[/math]-ben is benne van.
2. A probléma [math]P[/math]-ben van és [math]N P[/math]-teljes.
3. A probléma [math]N P[/math]-teljes és nincs [math]P[/math]-ben.
4. A probléma [math]P[/math]-ben van, de nincs [math]N P[/math]-ben.

Nézzük a következő két problémát: (2021 jan)

Legközelebbi pár: Adott [math]n[/math] szám egy rendezetlen tömbben. Határozzuk meg, hogy melyik két elem értéke van legközelebb egymáshoz. Legtávolabbi pár: Adott [math]n[/math] szám egy rendezetlen tömbben. Határozzuk meg, hogy melyik két elem értéke van legtávolabb egymástól. A megengedett lépések legyenek: két elem összehasonlítása, két elem távolságának (azaz különbségének) a meghatározása, két elemcseréje a tömbben.

Tekintsük a követkető állításokat:

A: A Legközelebbi pár feladat megoldható a cseréken túl [math]O(n \log n)[/math] lépésben.

B: A Legközelebbi pár feladat megoldható a cseréken túl [math]O\left(n^{2}\right)[/math] lépésben.

C: A Legtávolabbi pár feladat megoldható a cseréken túl [math]O(n)[/math] lépésben.

D: A Legtávolabbi pár feladat megoldható a cseréken túl [math]O(n \log n)[/math] lépésben.

Melyik helyes az alábbiak közül?

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. Csak az A.
2. Mind a négy igaz.
3. Csak az A, a B és a D.
4. Csak a B és a D.

Az [math]f(n)[/math] függvényről azt tudjuk, hogy [math]f(n) \in O\left(n^{2}\right)[/math] Az alábbiak közül melyik lehet [math]f[/math] ? (Mindegyik logaritmus kettes alapú.) (2020 jan)

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. [math]f(n)=3 \cdot 2^{(\log n)^{2}}+85 n^{2}[/math]
2. [math]f(n)=10 \cdot n \log n+12 n^{1,5}-8[/math]
3. [math]f(n)=3 n \log (n !)[/math]
4. [math]f(n)=20 \cdot \frac{n^{3}}{\log n}-15 n^{2}[/math]
5. Egyik sem lehet.

A kezdetben üres, [math]M=17[/math] méretü [math]A[/math] hash-táblába a [math]h(x) \equiv x(\bmod 17)[/math] hash-függvényt és lineáris próbát használva beraktunk 9 elemet, majd kitöröltük az egyiket. Ha tudjuk, hogy a törlés után a nem üres mezők tartalma (2020 jan)

A[3]=4, \quad A[4]=22, \quad A[5]=5, \quad A[7]=44, \quad A[9]=26, \quad A[10]=11, \quad A[11]=28, \quad A[16]=33,

akkor hol volt a törölt elem?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. [math]A[8][/math]-ban
2. [math]A[6][/math]-ban
3. [math]A[9][/math]-ben
4. Nem határozható meg.
5. Az elözőek egyike sem helyes.

Az angol ábécé 26 betűjéből és a 10 számjegyből hány olyan 8 hosszú sorozat készíthető, melyben sem két betü, sem két számjegy nem állhat egymás mellett? (Egy betü vagy számjegy többször is használható.) (2020 jan)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]26 \cdot 25 \cdot 24 \cdot 23 \cdot 10 \cdot 9 \cdot 8 \cdot 7[/math]
2. [math]2 \cdot\left[\left(\begin{array}{c}26 \\ 4\end{array}\right)+\left(\begin{array}{c}10 \\ 4\end{array}\right)\right][/math]
3. [math]2 \cdot 26^{4} \cdot 10^{4}[/math]
4. [math]26 \cdot 25 \cdot 24 \cdot 23+10 \cdot 9 \cdot 8 \cdot 7[/math]
5. Az előzőek egyike sem helyes.

Az alábbi gráfon a Kruskal-algoritmust használtuk minimális feszítőfa keresésre. Azt tapasztaltuk, hogy az algoritmus által kiválasztott első 3 él sorrendben a következő: [math]E C, D B, D E[/math] A felsorolt lehetőségek közül melyik lehet igaz az ismeretlen élsúlyokra? (2020 jan)

Hiba a bélyegkép létrehozásakor: Nem lehet a bélyegképet a célhelyre menteni

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]x=1, y=5[/math]
2. [math]x=5, y=1[/math]
3. [math]x=y[/math]
4. A fentiek egyike sem lehetséges.

A [math]G=(V, E)[/math] egyszerủ, irányítatlan gráf csúcsain adott egy [math]f: V \rightarrow\{0,1,2\}[/math] függvény. Melyik feltétel írja le azt, hogy ez a függvény a gráfnak egy szabályos 3 színnel való színezése? (2020 jan)

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. Minden [math]a, b \in V[/math] párra, ha [math]a \neq b[/math], akkor [math]f(a) \neq f(b)[/math]
2. Minden [math]a, b \in V[/math] párra, ha [math]\{a, b\} \in E[/math], akkor [math]f(a) \neq f(b)[/math]
3. Minden [math]a, b \in V[/math] párra, ha [math]f(a) \neq f(b)[/math], akkor [math]\{a, b\} \in E[/math]
4. Minden [math]a, b \in V[/math] párra, ha [math]\{a, b\} \notin E[/math], akkor [math]f(a)=f(b)[/math]

Tegyük fel, hogy [math]\mathrm{P} \neq \mathrm{NP}[/math] Tekintsük azt a problémát, amikor adottak az [math]a_{1}, a_{2}, \ldots, a_{n}[/math] pozitív egész számok, és azt kell eldönteni, hogy van-e olyan [math]I \subseteq\{1,2, \ldots, n\}[/math], melyre [math]\sum_{i \in I} a_{i}=2020[/math] (2020 jan)

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

Melyik állítás igaz az alábbiak közül?

1. A probléma P-ben és NP-ben is benne van.
2. A probléma P-ben van, de nincs NP-ben.
3. A probléma P-ben van és NP-teljes.
4. A probléma NP-teljes és nincs P-ben.

Tegyük fel, hogy [math]\mathrm{P} \neq \mathrm{NP}[/math] és jelölje [math]P_{1} \prec P_{2}[/math] azt, hogy a [math]P_{1}[/math] probléma Karp-redukálható (polinomiálisan visszavezethető) a [math]P_{2}[/math] problémára. Tekintsük az alábbi három problémát. (2020 jan)

Adott egy [math](G, k)[/math] pár, ahol [math]G[/math] egy irányítatlan gráf, [math]k[/math] egy pozitív egész és a kérdés az alábbi:

[math]\mathcal{A}[/math] : a [math]G[/math] gráfban van-e legalább [math]k[/math] pontból álló kör

[math]\mathcal{B}[/math] : a [math]G[/math] gráfban van-e legfeljebb [math]k[/math] pontból álló kör

[math]\mathcal{C}[/math] : a [math]G[/math] gráfban van-e pontosan [math]k[/math] pontból álló kör

Melyik állítás helyes az alábbiak közül?

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]\mathcal{C} \prec \mathcal{A}[/math] és [math]\mathcal{C} \prec \mathcal{B}[/math]
2. [math]\mathcal{A} \prec \mathcal{C}[/math] és [math]\mathcal{A} \prec \mathcal{B}[/math]
3. [math]\mathcal{B} \prec \mathcal{C}[/math] és [math]\mathcal{C} \prec \mathcal{A}[/math]
4. [math]\mathcal{A} \prec \mathcal{B}[/math] és [math]\mathcal{B} \prec \mathcal{C}[/math]

Legyen adott egy [math]G[/math] gráf, melynek adott két különböző csúcsa [math]A[/math] és [math]B[/math] Ez a két csúcs színtelen, a többi csúcs mindegyike vagy pirosra vagy kékre van színezve. (Szomszédos csúcsok lehetnek azonos színüek is.) Meg szeretnénk határozni a legkevesebb élú olyan utat [math]A[/math]-ból [math]B[/math]-be, ami csupa azonos színü csúcson megy át. Ehhez egy ismert algoritmust akarunk használni, akár többször is futtatva az alkalmas bemeneteken. (2020 jan)

Melyik helyes az alábbiak közül?

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. Irányított gráf esetében a Dijkstra-algoritmus segítségével a feladat megoldható, de szélességi kereséssel nem.
2. Irányított gráf esetében a Dijkstra-algoritmus segítségével és szélességi kereséssel is megoldható a feladat.
3. Irányítatlan gráf esetében sem a Dijkstra-algoritmus segítségével, sem szélességi bejárással nem oldható meg a feladat.
4. Irányított és irányítatlan gráf esetében sem oldható meg a feladat a Dijkstra-algoritmus segítségével, de szélességi kereséssel mindig megoldható.

Melyik feladatra nem ismert [math]O\left(n^{2}\right)[/math] lépésben müködő algoritmus? (2020 jan)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. Adott [math]n[/math] különböző egész szám közül a legkisebb kiválasztása.
2. Adott [math]n[/math] csúcsú bináris keresőfában tárolt elemek közül a legnagyobb meghatározása.
3. Adott [math]n[/math] bites [math]k[/math] egész számra [math]5^{k}[/math] kiszámolása.
4. Adott [math]n[/math] csúcsú, irányított, körmentes gráfban az adott [math]s[/math] csúcsból az adott [math]t[/math] csúcsba vezető legkevesebb élü út meghatározása.

Egy [math]n[/math] hosszú [math]s=s_{1} s_{2} \cdots s_{n}[/math] és egy [math]m[/math] hosszú [math]t=t_{1} t_{2} \cdots t_{m}[/math] sorozathoz a [math]T[/math] tömböt definiáljuk a következőképpen: Legyen [math]T[0, j]=T[i, 0]=0[/math] minden [math]1 \leq i \leq n[/math] és [math]1 \leq j \leq m[/math] estén, továbbá [math]T[0,0]=0[/math] Az [math]1 \leq i \leq n[/math] és [math]1 \leq j \leq m[/math] esetekben pedig (2020 jan)

[math]T[i, j]= \begin{cases}\max \{T[i, j-1], T[i-1, j], T[i-1, j-1]+1\} & \text { ha } s_{i}=t_{j} \\ \max \{T[i, j-1], T[i-1, j]\} & \text { ha } s_{i} \neq t_{j}\end{cases}[/math]

Legyen [math]n=100, m=20[/math], az [math]s[/math] az a 0 -val kezdődő sorozat, melyben az 1-ek és 0-k felváltva követik egymást, azaz [math]s=010101 \cdots 01[/math] és [math]t[/math] az a sorozat, melynek első tíz eleme 0 , a második tíz pedig 1 . Az alábbiak közül melyik állítás helyes?

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. [math]T[1,10]=15[/math]
2. [math]T[2,20]=2[/math]
3. [math]T[100,15]=10[/math]
4. Az előzőek egyike sem igaz.

Melyik az a legkisebb pozitív egész [math]d[/math] szám, melyre [math]f(n) \in O\left(n^{d}\right)[/math] teljesül, ha [math]f(n)=\sum_{k=1}^{n^{2}} \frac{k}{3}[/math]? (2019 jun)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. 2
2. 3
3. 4
4. 5
5. nincs ilyen d

Ha az alábbi bináris keresőfán végrehajtjuk a BESZÚR(15) műveletet, akkor az eredményül kapott bináris kereső́ára melyik állítás igaz? (2019 jun)

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

1. A 15 a gyökérben lesz.
2. A fa magassága nem változik meg.
3. A 15 egy olyan csúcsba kerül, ami gyereke a 12-es számot tartalmazónak.
4. Az előzőek egyike sem igaz.

Egy 200 csúcsú teljes páros gráfban az egyik oldalon a csúcsok 1-től 100-ig, a másik oldalon 101-től 200-ig vannak megszámozva. Hány olyan teljes párosítás található ebben a gráfban, amelyben minden páros csúcsnak páratlan, minden páratlannak pedig páros a szomszédja? (2019 jun)

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. [math]\frac{100 !}{2}[/math]
2. [math]\frac{100 !}{50 !}[/math]
3. [math]50 !+50 ![/math]
4. [math]50 ! \cdot 50[/math] !
5. Az előzőek egyike sem helyes.

Egy 6 csúcsú irányítatlan gráfon mélységi bejárást végeztünk. Az alábbi táblázat tartalmazza a csúcsok mélységi és befejezési számait. (2019 jun)

	A	B	C	D	E	F
mélységi	4	3	2	5	1	6
szélességi	4	1	5	2	6	3

Melyik élről állíthatjuk biztosan, hogy nem lehet a gráfban?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. [math](B, E)[/math]
2. [math](C, A)[/math]
3. [math](C, D)[/math]
4. [math](F, B)[/math]
5. A felsoroltak bármelyike előfordulhat.

Hat kártya van elöttünk az asztalon, tudjuk, hogy mindegyiknek az egyik oldalán egy betủ, a másik oldalán egy szám van. A következőket látjuk: [math]A, B, C, 1,2,3[/math]. (2019 jun)

Valaki azt állítja, hogy az is igaz, hogy minden mássalhangzó túloldalán páratlan szám szerepel. Ha minél kevesebb kártya megfordításával akarjuk ezt az állítást ellenőrizni, akkor melyik a jó módszer?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. Mind a hat kártyát megfordítjuk.
2. Csak a [math]B[/math] kártyát fordítjuk meg.
3. Csak a [math]B[/math] és [math]C[/math] kártyákat fordítjuk meg.
4. Az elözőek egyike sem helyes.

[math]\mathcal{A}: \quad \operatorname{Adott}[/math] egy [math]G[/math] irányítatlan gráf. (2019 jun)

Van-e [math]G[/math]-ben kör?

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]\mathcal{A}[/math] Benne van P-ben, de nincs benne NP-ben.
2. [math]\mathcal{A}[/math] Benne van NP-ben, de nincs benne P-ben.
3. [math]\mathcal{A}[/math] Benne van P-ben is és NP-ben is.
4. [math]\mathcal{A}[/math] Nincs benne P-ben se és NP-ben se.

[math]\mathcal{B}: \quad[/math] Adott egy [math]G[/math] irányítatlan gráf. (2019 jun)

Van-e [math]G[/math]-ben pontosan 2019 csúcsot tartalmazó kör?

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]\mathcal{B}[/math] Benne van P-ben, de nincs benne NP-ben.
2. [math]\mathcal{B}[/math] Benne van NP-ben, de nincs benne P-ben.
3. [math]\mathcal{B}[/math] Benne van P-ben is és NP-ben is.
4. [math]\mathcal{B}[/math] Nincs benne P-ben se és NP-ben se.

Tegyük fel, hogy [math]\mathrm{P} \neq[/math] NP és jelölje [math]P_{1} \prec P_{2}[/math] azt, hogy a [math]P_{1}[/math] probléma Karp-redukálható (polinomiálisan visszavezethető) a [math]P_{2}[/math] problémára. Tekintsük azt a két problémát, melyeknél adott egy [math](G, k)[/math] pár és (2019 jun)

[math]\mathcal{A}[/math] : a [math]G[/math] élsúlyozott gráfban van-e legfeljebb [math]k[/math] súlyú Hamilton-kör (2019 jun) ==

[math]\mathcal{B}[/math] : a [math]G[/math] gráfban van-e legalább [math]k[/math] pontú teljes részgráf

Melyik állítás helyes az alábbiak közül?

Típus: egy. Válasz: 1. Pontozás: nincs megadva.

1. [math]\mathcal{A} \prec \mathcal{B}[/math] és [math]\mathcal{B} \prec \mathcal{A}[/math]
2. [math]\mathcal{A} \prec \mathcal{B}[/math] és [math]\mathcal{B} \nprec \mathcal{A}[/math]
3. [math]\mathcal{A} \nprec \mathcal{B}[/math] és [math]\mathcal{B} \prec \mathcal{A}[/math]
4. [math]\mathcal{A} \nprec \mathcal{B}[/math] és [math]\mathcal{B} \nprec \mathcal{A}[/math]

Több különböző megbízás közül válogatunk, melyek mindegyikét adott napokon lehet elvégezni. Ha az [math]i[/math].ediket elvállaljuk, akkor a [math]k_{i}[/math] naptól a [math]v_{i}[/math] napig csak ezt csinálhatjuk. Legyen adott [math]n[/math] megbízás a hozzájuk tartozó [math]k_{i}[/math] és [math]v_{i}[/math] dátumokkal. Azt akarjuk eldönteni, hogy elvállalható-e közülük legalább [math]n / 2[/math] darab (mindegy, hogy melyikek). (2019 jun)

Melyik helyes az alábbiak közül?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

1. Tetszőleges irányított gráfban legrövidebb utat lehet polinom időben találni, és egy ilyen algoritmussal a feladat egyszerüen megoldható.
2. Tetszőleges irányított gráfban leghosszabb utat lehet polinom időben találni, és egy ilyen algoritmussal a feladat egyszerüen megoldható.
3. Irányított körmentes gráfban legrövidebb utat lehet polinom időben találni, és egy ilyen algoritmussal a feladat egyszerüen megoldható.
4. Irányított körmentes gráfban leghosszabb utat lehet polinom időben találni, és egy ilyen algoritmussal a feladat egyszerüen megoldható.

Melyik feladat oldható meg [math]O(n)[/math] lépésben? (2019 jun)

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. Tetszőleges [math]n[/math] különböző szám növekvő sorrendbe rendezése.
2. Annak ellenőrzése, hogy egy [math]n[/math] csúcsú gráf összefüggő-e.
3. Tetszőleges, [math]n[/math] elemet tároló bináris keresőfa alapján a tárolt elemek növekvő sorrendben való felsorolása.
4. Tetszőleges [math]n[/math] elemből egy bináris keresőfa építése.

Tekintsük a következő, az [math]a_{1}, a_{2}, \ldots, a_{n}[/math] paraméterektől függő rekurzív definíciót! Az [math](n+1) \times 1001[/math] tömbben (2019 jun)

[math]T[i, 0]=1[/math] ha [math]0 \leq i \leq n[/math]

[math]T[0, j]=0[/math] ha [math]1 \leq j \leq 1001[/math]

[math]T[i, j]=T[i-1, j][/math] ha [math]i \geq 1[/math] és [math]j \le a_{i}[/math]

[math]T[i, j]=\max \left\{T[i-1, j], T\left[i-1, j-a_{i}\right]\right\}[/math] ha [math]i \geq 1[/math] és [math]j \geq a_{i}[/math].

Legyen [math]a_{i}=3^{i-1}, i=1,2, \ldots[/math] Melyik igaz az alábbiak közül?

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

1. [math]T[2,15]=1[/math]
2. [math]T[3,9]=0[/math]
3. [math]T[3,10]=1[/math]
4. [math]T[20,3]=0[/math]
5. Az előzőek egyike sem igaz.