Számítógépes látórendszerek - Ellenőrző kérdések: Bináris képek
Tartalomjegyzék
- 1 Mit jelent a bináris kép? Mit jelent a küszöbözés? Milyen lehetőségeink vannak? Mit jelent a dupla-küszöbözés?
- 2 Ismertesse a bináris képen végezhető logikai műveleteket és azok fontosabb feladatait. Ismertesse az objektum alapú logikát és felhasználási lehetőségeit.
- 3 Mit jelent az erózió és a dilatáció? Hogyan végzünk nyitást és zárást? Mire jók ezek a műveletek, mitől függ, hogy melyiket alkalmazzuk? Hogyan tudunk e műveletekkel kontúrt keresni? Mi az olvasztásmentes dilatáció? Szürkeárnyalatos képen hogy lehet értelmezni ezeket a műveleteket?
- 4 Mit jelent a 4- és 8-szomszédú távolság? Mik az előnyei és hátrányai az euklideszi távolsághoz képest?
- 5 Ismertesse a csontváz definícióját és a csontvázasítás egy lehetséges megvalósítását.
- 6 Hogyan tudunk bináris képen objektumokat keresni és megszámlálni? Ismertesse az eljárásokat.
Mit jelent a bináris kép?
Mit jelent a küszöbözés?
Milyen lehetőségeink vannak?
Mit jelent a dupla-küszöbözés?
Bináris kép
Minden pixel csak két értéket vehet fel (megjelenítés tipikusan fekete/fehér színnel). A pixelekhez hozzárendelendő értéket valamilyen képi tulajdonság (fényerő, színintenzitás stb.) küszöbözésével határozzuk meg.
Küszöbözés (thresholding)
A legegyszerűbb eljárás, aminek segítségével egy szegmentálást (objektum(ok) és a háttér szétválasztása) végezhetünk. Egy tulajdonsághoz hozzárendelünk küszöbértéket, majd a vizsgálandó kép minden pixelén végigmegyünk és összehasonlítjuk az értékeket. A végeredmény egy bináris kép.
Például fényintenzitás alapján bizonyos érték fölött és alatt szétválasztom a képet.
Hisztogram
Hisztogram egy kép egy adott tulajdonságáról (előfordulás: az adott értékkel ennyi számú pixel rendelkezett):
Szegmentálási lehetőségek
- Hisztogram alapú -> KÜSZÖBÖZÉS
- Osztályozás alapú
- Színek
- Formák: pl.:egyenes, kör
- Környezetfüggő
- Lokális: inhomogén háttér esetén
Dupla-küszöbözés
Más néven hiszterézises küszöbözés. A probléma az, hogy elkülönítendő objektumok mellett más hasonló (kinézetű, színű stb) objektumok is vannak, melyek küszöbözés után megmaradnak. Ezért kettő küszöb használatával létrehozunk két képet, melyet aztán ÉS kapcsolatba helyezünk.
Példa
- Eredeti kép
- Eredeti kép küszöbözése
- Eredeti képen élkeresés
- Élkeresett kép küszöbözése
- „4” maszkolása „2”-vel
Ismertesse a bináris képen végezhető logikai műveleteket és azok fontosabb feladatait.
Ismertesse az objektum alapú logikát és felhasználási lehetőségeit.
Adott két kép: A, B
- Negálás: például kontúrkeresésnél
- AND: főleg képek maszkolásánál van jelentősége, két kép átfedésének megjelenítése
- OR:
- XOR:
Mit jelent az erózió és a dilatáció? Hogyan végzünk nyitást és zárást? Mire jók ezek a műveletek, mitől függ, hogy melyiket alkalmazzuk? Hogyan tudunk e műveletekkel kontúrt keresni? Mi az olvasztásmentes dilatáció? Szürkeárnyalatos képen hogy lehet értelmezni ezeket a műveleteket?
Erózió
Csökkentés (fehér területek csökkentése fekete-fehér átmeneteknél). A pixelszerű zajok csökkentése.
Dilatáció
Szélesítés (fehér területek növelése fekete-fehér átmeneteknél)
A változás mértéke függ a felhasznált kernel nagyságától. Nagy számításigény.
A nulla zajokat tüntetem el, cserébe megnő az objektum mérete.
Példa: 1D-s eset
Zárás
Dilatáció + erózió: nullzajok kiszedése (fekete pöttyök, fekete vonalak)
Nyitás
Erózió + dilatáció: fehér pixelhibák kiszedésére
(Gyakran együtt használják a kettőt.)
(Az előadásdiákon pont fordítva szerepel a nyitás és a zárás, de minden más forrásban a fentiek szerint van megadva.)
Felhasználás
- pixelhibák, pixelszerű zajok eltüntetése bináris képről
- kontúrkeresés: Img AND INVERSE( dilate(Img) )
- élkeresés és lyukak kitöltése
Olvasztásmentes dilatáció
Egymással érintkező objektumok éldetektálásánál segít ez a módszer.
Szürkeárnyalatos képen:
- erózió: minimum szűrő (sötétít)
- dilatáció: maximum szűrő (világosít)
Mit jelent a 4- és 8-szomszédú távolság? Mik az előnyei és hátrányai az euklideszi távolsághoz képest?
Kernelek esetén a kernel középpontjától a pixelekben mért távolság a szélek felé haladva.
- 4/8 szomszéd: gyors, pontatlan
- EDM: pontos, számításigényesebb
Ismertesse a csontváz definícióját és a csontvázasítás egy lehetséges megvalósítását.
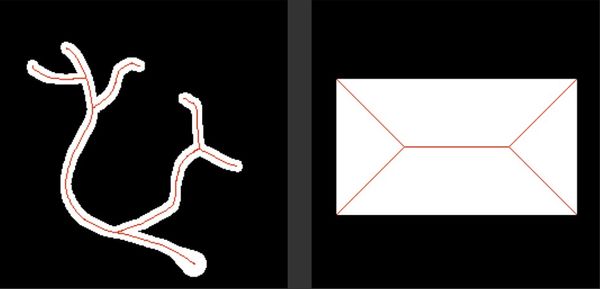
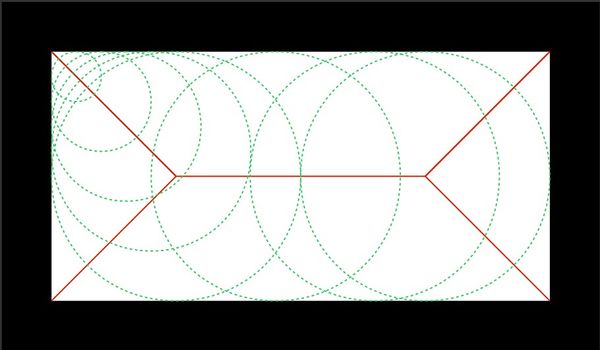
Definíció: Maximális körök origója mely egy adott objektumba helyezhető.
Megvalósítás:
Felhasználás: ujjlenyomat ellenőrzés
Hogyan tudunk bináris képen objektumokat keresni és megszámlálni? Ismertesse az eljárásokat.
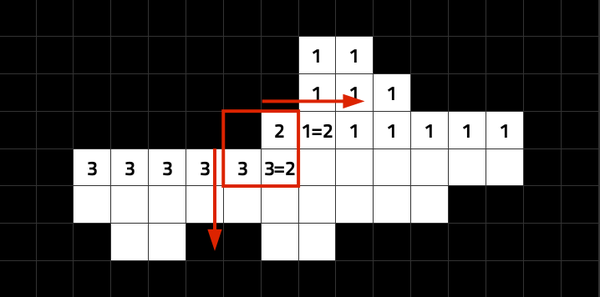
Objektumkeresés
Egy 2x2-es ablakkal végigpásztázunk minden pixelt és indexeljük az egyes pixeleket.
|
Új index |
|
Másolás |
|
Másolás | ||||||||||||
|
Egyesítés |
|
Új index |
|
Másolás |
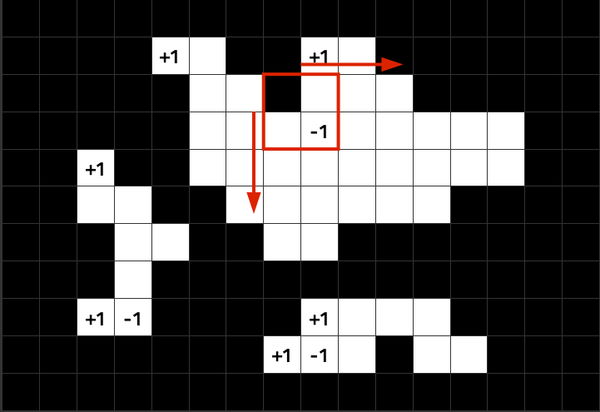
Objektumszámlálás
Egy 2x2-es ablakkal végigpásztázunk minden pixelt és növeljük, vagy csökkentjük (hogy az algoritmus ne számoljon egy objektumot többször) a számlálónk értékét.
|
+1 |
|
-1 |
|
+1 |