Matematika A3 - Vizsgakérdések az elégségesért

Ez az oldal a korábbi SCH wiki-ről lett áthozva. Az eredeti változata itt érhető el.

Ha úgy érzed, hogy bármilyen formázási vagy tartalmi probléma van vele, akkor kérlek javíts rajta egy rövid szerkesztéssel.

Ha nem tudod, hogyan indulj el, olvasd el a migrálási útmutatót

Nguyen Xuan Ky, Serény György, Tóth János

BME TTK Algebra és Matematikai Analízis Tanszék

2006. december 5.

Aki elérte a 40-54 százalékot, az szóbelizik a kettesért. Javaslat: kapjon egy-egy kérdést, és ha kettőre válaszol, menjen át.

---

Ha tudod valamelyikre a választ, írd bele!

1. Differenciálegyenletek

1. Mit nevezünk homogén egyenletnek? Mit nevezünk homogén lineáris differenciálegyenletnek?

y'(x)+a(x)y(x)=b(x), ahol b(x)=0. Lineáris, ha a polinómfüggvény minden tagjának azonos a fokszáma. Homogén: nem szerepel konstans, vagy csak a független változót tartalmazó tag.

Amúgy meg: http://www.sosmath.com/diffeq/first/homogeneous/homogeneous.html

2. Mit nevezünk közvetelnül integrálható differenciálegyenletnek?

Ahol az előbbi egyenletben a(x)=0.

3. Mit nevezünk autonóm differenciálegyenletnek?

? G(y(x))-G(y0)=x-c ? Autonóm differenciál egyenletnek nevezzük azt a közönséges diffegy-et, amely nem függ független változóktól. http://en.wikipedia.org/wiki/Autonomous_differential_equation

4. Mit nevezünk szétválasztható változójú egyenletnek?

Általános alak: y'=g(x)*h(y).

5. Mit nevezünk elsőrendű lineáris differenciálegyenletnek?

Elsőrendű: csak 1. deriváltak szerepelnek, lineáris: az ismeretlen függvénynek és deriváltjának csak 1. hatványa szerepel, és nem szerepel a szorzatuk.

6. Az állandók variálásának módszere?

Az elsőrendű lineáris inhomogén differenciálegyenlet partikuláris megoldása az állandó variálásának módszerével kapható meg. Az inhomogén egyenlet y0 partikuláris megoldását a homogén egyenlet már ismert általános megoldásához hasonló szerkezetűnek tételezzük fel, csak az abban szereplő C állandót most egy C(x) függvénynek képzeljük. Az eredeti egyenletbe visszahelyettesítve megkapjuk C(x)-et.

7. Milyen elégséges feltételt ismer kezdeti érték problémák megoldásának létezésére?

Ha a kezdeti érték feltétel [math] m(0)= M e^{-kt} \,\,\, t \in \mathbb{R} [/math] alakú. Az alábbi feltétel leszámítva a Lipschitz feltételt ha teljesül akkor létezik megoldás.

8. Milyen elégséges feltételt ismer kezdeti érték problémák megoldásának létezésére és egyértelműségére?

Cauchy-Lipschitz feltétel: ha az n+1 változós függvény az n+1 dimmenziós tér valamely zárt korlátos tartományán folytonos, és éppen a részhalmazon legfeljebb az első változót leszámítva eleget tesz a Lipschitz-feltételnek, akkor az y^(n)=(x,y,ydeivált,...,y n-1. deriváltja) differenciálegyenlethez és a tartomány egy belső pontjához a kezdeti érték probléma egyértelműen megoldható. Lipschitz feltétel: abszolutérték (f(x,y1)-f(x,y2))>=abszolutérték (y2-y1)

9. Mit nevezünk kontrakciónak?

Zsugorítást. ha d(T(x),T(y))<qd(x,y) és q[0,1[, akkor T operátor kontrakció.

10. Mi az Euler-módszer lényege?

y'(x)=f(x,y(x)) y_hullam(x0+h)=y0+hf(x0,y0) y_hullam(x0+2h)=y0(x0+h)+hf(x0,y_hullam(x0+h))

11. Milyen függvények esetén értelmezhető a Laplace-transzformáció?

Az olyan függvények esetén, ahol az a jól ismert improprius integrál létezik, és minden P esetén éppen az improprius integrál értékét adja vissza függvényértékként.

12. Számolja ki egy függvény deriváltjának Laplace-transzformáltját!

Ha [math] \mathcal{L}\left(f(x)\right) = F(p) [/math], akkor [math] \mathcal{L}\left(f'(x)\right) = p \cdot F(p) - f(0)[/math]

13. Mikor mondjuk, hogy az [math] F(x; y(x)) + y'(x)G(x; y(x)) = 0[/math] differenciálegyenlet egzakt?

A diffegyenlet akkor egzakt, ha F y szerinti parciális deriváltja egyenló G x szerinti parciális deriváltjával. Azaz [math]\frac{\partial F}{\partial y} = \frac{\partial G}{\partial x}[/math]

14. Mit nevezünk integráló tényezőnek?

Integráló tényezővel megszorozva a differenciálegyenletet, az egzakttá tehető.

15. Mit nevezünk iránymezőnek?

Az y'=f(x,y) differenciálegyenlet megoldása geometriailag a következőkéépen szemléltethető. Az f függvény értelmezési tartományának minden egyes (x,y) pontjához rendeljük hozzá a rajta átmenő y'=f(x,y) iránytangensű egyenesnek a pontot tartalmazó "kicsiny" szakaszát. Ezen szakaszok összessége a differenciálegyenlet iránymezőjét alkotja. A szakaszokból elég sokat ábrázolva kapjuk a differenciálegyenlet megoldásának geometriai képépt.

16. Mit nevezünk irányvonalnak vagy izoklínának?

Azt a görbét, amelynek a pontjaihoz azonos irányú, azaz párhuzamos vonalelemek tartoznak, izoklínának (izoklína görbének) nevezzük. Tehát az izoklína olyan vonal, amelynek minden pontjában y' értéke ugyanaz.

2. Vektoranalízis

1. A gradiens definíciója és kiszámításának módja?

A gradiens a skalártér növekedésének nagyságát és irányát adja meg.

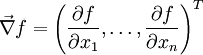
http://en.wikipedia.org/wiki/Gradient

2. A rotáció definíciója és kiszámításának módja?

A rotáció a vektortérben található hurkokat méri.

Rotáció: a deriváltoperátor vektorinvariánsának a kétszerese. Kiszámítása: [math]\displaystyle{} rot \rm v(x,y,z) = \left|\begin{array}{ccc}\underline{i} & \underline{j} & \underline{k} \\ \partial_x & \partial_y & \partial_z \\ v_x & v_y & v_z\end{array}\right| = \left(\frac{\partial v_z}{\partial_y} - \frac{\partial v_y}{\partial_z} ; \frac{\partial v_x}{\partial_z} - \frac{\partial v_z}{\partial_x} ; \frac{\partial v_y}{\partial_x} - \frac{\partial v_x}{\partial_y}\right)[/math]

http://en.wikipedia.org/wiki/Curl

3. A divergencia definíciója és kiszámításának módja?

A divergencia a vektortérben egy pontból kiinduló vagy egy pontban összefutó erõvonalak (források és nyelõk) mennyiségi jellemzõje A deriváltoperátor skalárinvariánsa

http://hu.wikipedia.org/wiki/Divergencia_%28vektoranal%C3%ADzis%29

4. A vonalintegrál definíciója és kiszámításának módja?

[math] \int\limits_r v \mathrm{d}r = \int\limits_t v(r(t)) * r'(t) \mathrm{d}t[/math]

http://en.wikipedia.org/wiki/Line_integral

5. Adja meg a csavarvonal paraméteres alakját!

[math] r(t)=Rcost\underline{i} + Rsint\underline{j} + ct\underline{k} [/math]

6. Mit nevezünk egy görbe ívhossz szerinti paraméterezésének?

[math]s= \int_{t1}^{t2} | r'(t)| dt[/math]

7. Mit nevezünk tenzornak?

Ha a v vektormező additív és homogén, akkor tenzornak nevezzük. A tenzor lineáris operátor=összeg és aránytartó. Vektor-vektor típusú leképezéseknél alkalmazzuk. v=rA Additív: v(x1+x2,y1+y2,z1+z2)=v(x1,y1,z1)+v(x2,y2,z2)

Homogén: v(ax,ay,az)=a*v(x,y,z)

http://hu.wikipedia.org/wiki/Tenzor

8. Mit nevezünk egy tenzor skalárinvariánsának?

A mátrix rangja, a főátló elemösszege, a főátló aldeterminánsösszege, a mátrix determinánsa. Független az alapvektorrendszertől.

10. Mit nevezünk egy vektormező skalárpotenciáljának?

V vektorfüggvénynek U skalárfüggvény skalárpotenciálja, ha gradU=V

http://en.wikipedia.org/wiki/Scalar_potential

11. Mit nevezünk egy vektormező vektorpotenciáljának?

V vektorfüggvénynek U vektorfüggvény skalárpotenciálja, ha v(r)=rot(u(r))

http://en.wikipedia.org/wiki/Vector_potential

12. Mi jellemzi a potenciálos erőtereket?

Ha [math] rot \underline{v}(r)=0 [/math] akkor potenciálos, tehát zárt görbén [math] \int \underline{v}(r) \mathrm{d}r=0. [/math]

13. Mit nevezünk egyszeresen összefüggő tartománynak?

Olyan tartományt, melyen bármely zárt görbe belseje is része a tertománynak

14. Mit nevezünk fluxusnak?

Egy vektorfüggvény valamely felületre vonatkozó felületi integrálja a felületre vonatkozó fluxusa

http://en.wikipedia.org/wiki/Flux

16. Mit mond ki a Newton-Leibniz-tétel három dimenzióban?

[math]\int_{a}^b v'(x) \mathrm{d}x = \int\limits_V div \, \underline{v} \, \mathrm{d}V = \int\limits_{F1} \, \underline{v} \, \mathrm{d}f + \int\limits_{F2} \, \underline{v} \, \mathrm{d}f = v(b) -v(a)[/math]

Fizikai jelentése: Egy cső két végén be- és kiáramló folyadék mennyiségének különbsége a csőben keletkező és eltűnő folyadák mennyiségével egyenlő, amely nem más, mint a hosszegységenként keletkező (eltűnő) folyadékmennyiségnek, azaz a hosszegységenkénti folyadékmennyiség-változásnak a cső hosszára vett integrálja.�

17. Mit mond ki a Gauss-Osztrogradszkij-tétel?

A Gauss�-Osztogradszkij tétel a Newton-Leibniz tétel többdimenzióra való általánosítása. Egy vektormező zárt felületen vett integrálja egyenlő a vektormező divergenciájának a térfogaton vett integráljával.

[math]\iint\limits_F \underline{v} \, dF = \iiint\limits_V div \, \underline{v} \, dV[/math]

http://en.wikipedia.org/wiki/Divergence_theorem

18. Mit mond ki a Green-tétel?

http://en.wikipedia.org/wiki/Green_theorem

19. Mit mond ki a Stokes-tétel?

Egy vektormező zárt vonalmenti integrálja egyenlő a vektormező rotációjának a felületen vett integráljával. (ugye ez az?)

[math]\int\limits_G \underline{v} \, dG = \iint\limits_F rot \, \underline{v} \, dF[/math]

http://en.wikipedia.org/wiki/Stokes_theorem

20. Mi jellemzi az örvénymentes vektormezőket?

a) v potenciálos rot v(r) = 0, bármely zárt görbén vett integrál 0 b) örvénymentes c) konzervativ [math] \int\limits_L r dr = 0 [/math]

21. Mi jellemzi a forrásmentes vektormezőket?

a) div v = 0 b) v vektormezo vektorpotencialja omega, ha v = rot omega c) minden zárt felületre a fluxus = 0, [math] \oint\oint\limits_F \underline{G} df=0[/math]

3. Komplex függvénytan

3. Mit mondanak ki a Cauchy-Riemann egyenletek?

[math]\displaystyle{} \frac{\partial U}{\partial x} = \frac{\partial V}{\partial y} [/math]

[math]\displaystyle{} \frac{\partial U}{\partial y} = - \frac{\partial V}{\partial x} [/math]

Szükséges, de nem elégséges feltételek z=u(x,y)+jv(x,y) totális diffhatóságára.

http://en.wikipedia.org/wiki/Cauchy_Riemann_equations

4. Mikor nevezünk egy komplex függvényt regulárisnak?

Egy függvény reguláris egy pontban, ha létezik olyan környezete, melyben differenciálható (a pontban is)

http://en.wikipedia.org/wiki/Meromorphic_function

5. Mikor nevezünk egy többváltozós függvényt harmonikusnak?

Ha teljesül a laplace egyenlet: deriváljuk kétsze x szerint, kétszer y szerint, és ha ezek összege 0 akkor teljesül.

http://en.wikipedia.org/wiki/Harmonic_function

6. Mit nevezünk egy függvény harmonikus párjának?

http://en.wikipedia.org/wiki/Harmonic_conjugate

Olyan függvényt, mellyel együtt reguláris függvényt alkot

7. Milyen függvénynek van harmonikus párja?

Ha egy függvény harmónikus T egyszeresen összefüggő tartományon, akkor van harmónikus társa t-n

11. Hogyan értelmezzük a komplex kitevős hatványokat?

[math] a^{z} = a^{x} * a^{jy} [/math]

14. Vonalintegrálokra vonatkozó Newton–Leibniz-tétel?

[math] \exists F: F'(z)=f(z) \,[/math] [math] \forall z \in T[/math], ahol tetszőleges (nyílt, összefüggő) tartomány [math]L \in T \Rightarrow \int f(z) dz=F(B)-F(A) [/math]

15. Mit mond ki Cauchy tétele?

Ha f reguláris az egyszeresen összefüggő tartományon, akkor bármely T-beli egyszerű zárt görbére: [math] \int f(z)dz=0[/math]

16. Mit mond ki a Cauchy-féle integráltétel?

Ha f reguláris az egyszeresen összefüggő T tartományon, akkor bármely [math] L \subset T [/math] sima egyszerű zárt görbére [math]\int\limits_L \, f = 0[/math] (FIXME: itt lehet, hogy az integrálforumlára gondolt?)

17. Mit nevezünk egy Laurent-sor fő részének?

Főrész: A negatív kitevőjű tagokat tartalmazó rész.

18. Mit nevezünk izolált szingularitásnak?

Olyan szingularitás (a függvény nem értelmezett pontja), amelynek tetszőlegesen kis környezetében a függvény értelmezve van.

19. Mit nevezünk megszüntethető szingularitásnak?

ha lim z>z0 f(z)=A komplex szám

20. Mit nevezünk n-edrendű pólusnak?

pólus ha lim z>z0 f(z)=végtelen, és n-ed rendű ha lim z>z0 (z-z0)^nf(z)=A!=0

21. Mit nevezünk lényeges szingularitásnak?

ha lim z>z0 f(z) nem létezik, sem véges sem végtelen határérték

22. Hogyan látszik az a körüli Laurent-soron, hogy a megszüntethető szingularitás?

Nincs főrésze, azaz nem tartalmaz negatív kitevőjű hatványokat, tehát 0-tól szummázunk.

23. Hogyan látszik az a körüli Laurent-soron, hogy a n-edrendű pólus?

Véges sok tagból álló főrésszel rendelkezik, vagyis n-től szummázunk.

24. Hogyan látszik az a körüli Laurent-soron, hogy a lényeges szingularitás?

Végtelen sok tagból álló főrésze van: - végtelentől +végtelenig szummázunk

25. Mi az f függvény reziduuma az a pontban?

Res(f,a)=c^-1. A Laurent-sor c^-1 együtthatóját az f függvény z-a helyhez tartozó rezidumának nevezzük.

26. Hogyan számítható ki a reziduum a Laurent-sor együtthatóiból?

A reziduum a Laurent-sorban a [math]z^{-1}[/math]-es tag szorzója. Pl. [math]L = 2z+\frac{3}{z}+\frac{5}{z^2}+...[/math] esetén Res=3.

27. Hogyan számítható ki a reziduum elsőrendű pólusban?

lim z>z0 (z-z0)f(f)

29. Mit mond ki a reziduumtétel?

http://en.wikipedia.org/wiki/Residue_theorem

-- Robi - 2007.01.12.