„Algoritmuselmélet - ZH, 2013.04.03.” változatai közötti eltérés
| (21 közbenső módosítás, amit 4 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| + | {{Vissza|Algoritmuselmélet}} | ||
| + | |||
==2013.04.03. ZH megoldásai== | ==2013.04.03. ZH megoldásai== | ||
| − | ===1. Feladat=== | + | ===1. Feladat (Van megoldás)=== |
| − | + | Mi az a legkisebb ''r'' racionális szám, melyre teljesül, hogy <math>\sqrt{1} + \sqrt{2} + \sqrt{3} + ...+\sqrt{n} = O(n^{r}) ?</math> | |
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
| + | *Először megpróbáljuk felülről becsülni: | ||
| + | **Felülről becsüljük a sorozatot, ha az elemeket rendre <math>\sqrt{n}</math>-nek tekintjük, vagyis:<br><br> | ||
| + | **<math>\sqrt{n} + \sqrt{n} + \sqrt{n} + ...+\sqrt{n}=n\cdot\sqrt{n}=n^{1.5}=O(n^{1.5}) \Rightarrow r=1.5</math><br><br> | ||
| + | *Most pedig megpróbáljuk alulról becsülni: <br><br> | ||
| + | **Alulról becsüljük a sorozatot: <br><br> | ||
| + | **<math> \frac{n}{2 } \cdot \sqrt{1}+\frac{n}{2} \cdot \sqrt{n} \leq \sqrt{1} + \sqrt{2} + \sqrt{3} \dots \sqrt{n} </math> <br><br> | ||
| + | **<math> \frac{n}{2 } \cdot \sqrt{1}+\frac{n}{2} \cdot \sqrt{n} = O(n^{1.5}) \Rightarrow r=1.5. </math> <br><br> | ||
| + | *A kettőt együttvéve látszik, hogy <math> r = 1.5 .</math> | ||
| − | |||
}} | }} | ||
| − | ===2. Feladat=== | + | ===2. Feladat (Van megoldás)=== |
| − | + | Egy <math> A[i,j] </math> <math>n</math> x <math>n</math>-es táblázat minden mezőjében egy egész szám van írva (nem feltétlenül csak pozitívak). Adjon <math> O(n^2) </math> lépésszámú algoritmust, ami eldönti, hogy melyik az a téglalap alakú része a táblázatnak, melynek bal felső sarka egybe esik a nagy táblázat bal felső sarkával és benne az elemek összege az egyik legnagyobb. | |
| + | |||
| + | (Vagyis olyan <math>k, l</math>-t keresünk, amire <math> \sum_{i \leq k, j \leq l}A[i,j] </math> maximális.) | ||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
| − | + | {{Rejtett | |
| + | |mutatott=<big>''Megjegyzések a feladathoz''</big> | ||
| + | |szöveg= | ||
| + | |||
| + | *Ahogy az többször is segít, úgy most is, hogy felrajzolunk magunknak egy 3x3, vagy 4x4-es táblázatot, és nézegetjük, hogyan kéne dolgozni... | ||
| + | *A feladatban 1-1 lépésnek vettem: | ||
| + | **1 művelet (<math> +,- </math>) elvégzését ''(vagyis a <math> B[i,j]=B[i-1,j]+B[i,j-1]+A[i,j]-B[i-1,j-1] </math> 3 lépés).'' | ||
| + | **1 értéke beírása a cellába. | ||
| + | **1 összehasonlítás (és esetleges cserék). | ||
| + | |||
| + | }} | ||
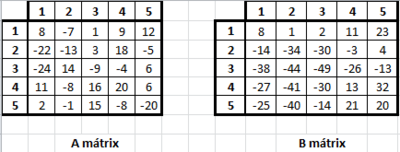
| + | *Adott az <math> A </math> mátrix. | ||
| + | *Létrehozunk egy <math> B </math> mátrixot (szintén <math>n</math> x <math>n</math>-es).''(ez <math>\Rightarrow O(n^2)</math> lépés)'' | ||
| + | *<math> B[1,1]:= A[1,1]</math>. ''(ez <math>\Rightarrow 1 </math> lépés)'' | ||
| + | *<math> k=l=1 </math> és <math> aktmax=B[1,1] </math>. | ||
| + | *Először kitöltjük az 1. sort <math> \rightarrow B[i,1]:=B[i-1,1]+A[i,1], i=2 \dots n </math>. ''(ez <math>\Rightarrow 2(n-1)=O(n)</math> lépés)'' | ||
| + | *Majd kitöltjük az 1. oszlopot <math> \rightarrow B[1,i]:=B[1,i-1]+A[1,i], i=2 \dots n </math>. ''(ez <math>\Rightarrow 2(n-1)=O(n)</math> lépés)'' | ||
| + | *Minden további cellában pedig <math> B[i,j]=B[i-1,j]+B[i,j-1]+A[i,j]-B[i-1,j-1] </math>. ''(ez <math>\Rightarrow 4(n-1)(n-1)=O(n^2)</math> lépés)'' | ||
| + | *A keresett <math> k,l </math> párost pedig folyamat nyilván tartjuk: ha <math> B[i,j] \geq aktmax \Rightarrow k=i, l=j, aktmax = B[i,j] </math>. ''(ez <math>\Rightarrow n^2-1=O(n^2)</math> lépés)'' | ||
| + | *<math> 1+2O(n)+ 3O(n^2)=O(n^2)</math> lépésszámú algoritmusunk van, tehát jók vagyunk. | ||
| + | :::::::::::::::::[[File:Algel zh 2013tavasz A B matrix.PNG|400px]] | ||
| + | |||
}} | }} | ||
| 25. sor: | 57. sor: | ||
{{Rejtett | {{Rejtett | ||
| − | |mutatott=<big>'' | + | |mutatott=<big>''Megjegyzések a feladathoz''</big> |
|szöveg= | |szöveg= | ||
*Szokásos rendezést használó bináris keresőfa: <math>bal(x) < x < jobb(x)</math> | *Szokásos rendezést használó bináris keresőfa: <math>bal(x) < x < jobb(x)</math> | ||
*Postorder: | *Postorder: | ||
| − | **Rekurzívan <math> bal(x) \rightarrow jobb(x) \rightarrow x </math>. Magyarul előbb meglátogatja a gyökérnél kisebbeket, utána a nagyobbakat, és ezután jön csak a gyökér. | + | **Rekurzívan <math> bal(x) \rightarrow jobb(x) \rightarrow x </math>.''(Magyarul: előbb meglátogatja a gyökérnél kisebbeket, utána a nagyobbakat, és ezután jön csak a gyökér.)'' |
**Egyik fontos tulajdonsága, hogy a '''gyökér''' az mindig a ''(figyelt)'' '''lista végén van'''. | **Egyik fontos tulajdonsága, hogy a '''gyökér''' az mindig a ''(figyelt)'' '''lista végén van'''. | ||
}} | }} | ||
| 37. sor: | 69. sor: | ||
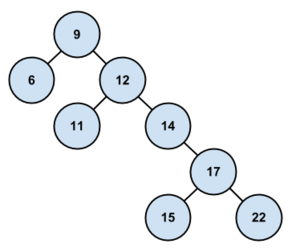
**Az 1. sorban a 9 lesz a gyökér. Felrajzoljuk a 9-t gyökérnek. ''(Bal oldalt lesz a hiba, de gyakorlásképp nézzük inkább a jobb oldalt.)'' | **Az 1. sorban a 9 lesz a gyökér. Felrajzoljuk a 9-t gyökérnek. ''(Bal oldalt lesz a hiba, de gyakorlásképp nézzük inkább a jobb oldalt.)'' | ||
**A 2. sorban a 12 lesz a gyökér, így a 12-est felrajzoljuk a 9-es jobb fiának. Nála csak a 11 a kisebb (a vizsgált listában), így a 11-t berajzoljuk a 12 bal fiának. | **A 2. sorban a 12 lesz a gyökér, így a 12-est felrajzoljuk a 9-es jobb fiának. Nála csak a 11 a kisebb (a vizsgált listában), így a 11-t berajzoljuk a 12 bal fiának. | ||
| − | **A 3. sorban 14 lesz a gyökér, így | + | **A 3. sorban 14 lesz a gyökér, így a 14-est felrajzoljuk a 12-es jobb fiának. |
**A 4. sorban a 17 lesz a gyökér, így ez a 14-es jobb fia lesz. A 15 és 22 pedig értelemszerűen a bal, és jobb fia lesz 17-nek. | **A 4. sorban a 17 lesz a gyökér, így ez a 14-es jobb fia lesz. A 15 és 22 pedig értelemszerűen a bal, és jobb fia lesz 17-nek. | ||
**Az 5. sorban a gyökér a 6 lesz, így azt berajzoljuk a 9-es bal fiának. És itt látszik is, hogy hiba van, hiszen <math> < > < </math> sorrend van, ebből következik, hogy ilyen fa nem létezhet. | **Az 5. sorban a gyökér a 6 lesz, így azt berajzoljuk a 9-es bal fiának. És itt látszik is, hogy hiba van, hiszen <math> < > < </math> sorrend van, ebből következik, hogy ilyen fa nem létezhet. | ||
| − | ::::::::::[[File: | + | ::::::::::[[File:Algel zh 2013tavasz Post tabla.png|400px]] [[File:Algel zh 2013tavasz Graf.png|300px]] |
}} | }} | ||
| − | ===4. Feladat=== | + | ===4. Feladat (Van megoldás)=== |
| − | + | Adjacencia-mátrixával adott <math>n</math> csúcsú, irányított gráfként ismerjük egy város úthálózatát. El szeretnék jutni <math>A</math> pontból <math>B</math> pontba, de sajnos minden csomóponthoz várnunk kell a nagy hóesés miatt, a várakozás hossza minden csomópontra ismert és független attól, hogy merre akarunk továbbmenni. Adjon algoritmust, ami <math>O(n^2)</math> lépésben eldönti, hogy merre menjünk, hogy a lehető legkevesebbet kelljen várni összességében. ''(A csomópontok közötti utak hosszának megtétele a várakozáshoz képest elhanyagolható időbe telik, tekintsük 0-nak. <math>A</math>-ban és <math>B</math>-ben nem kell várakozni.)'' | |
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
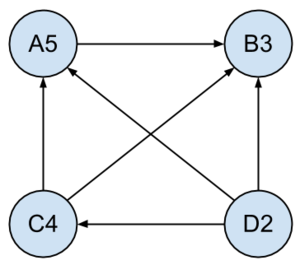
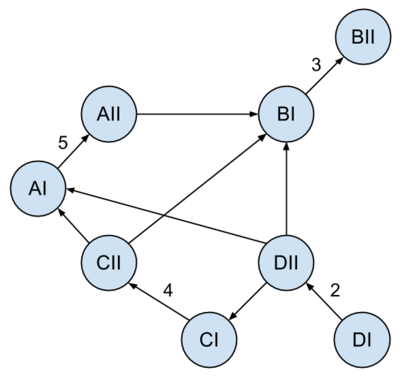
| − | + | *A "probléma", hogy a csúcsoknak van súlya (ill. az éleknek is van, de az 0), amivel nem igen tudunk mit kezdeni. De nem hiába volt BSZ1 (vagy BSZ2?), ahol megtanultuk, hogy könnyedén csinálhatunk a csúcssúlyból élsúlyt. | |
| + | *Az adott pontot (X) lecseréljük 2 pontra (X1, X2). Ami eddig X-be ment, az menjen X1-be, és ami X-ből ment, az menjen X2-ből. ''(Vagyis X1-ből csak X2-be megy él, és X2-be csak az X1 megy.)'' | ||
| + | *A 2 pontot összekötjük, a köztük menő élsúly pedig az X pont súlya lesz. | ||
| + | *Csináljuk hát ezt ezzel a gráffal: | ||
| + | **Az eredeti <math> n </math> csúcsú G gráfból csinálunk így egy F gráfot, melyben <math> 2n </math> csúcs lesz ''(és az élszám is n-nel nő, de ez most minket annyira nem izgat)''. | ||
| + | **Ebben az F gráfban kell megtalálni a legrövidebb utat egy "X2"-ből egy "Y1"-be. | ||
| + | **A Dijkstra-algoritmus <math> O(n^2) </math> lépésben keres legrövidebb utat, ebben az esetben <math> O((2n)^2)=4O(n^2)=O(n^2)</math>. | ||
| + | *Így a feladat ezzel meg is oldva. | ||
| + | ::::::::::[[File:Algel zh 2013tavasz Csucs suly.png|300px|G gráf]][[File:Algel zh 2013tavasz El suly.png|400px|F gráf]] | ||
| + | |||
| + | Talán egyszerűbben: mivel 0 az utazási idő (élsúlyok) és bármerre megyünk egy csúcsból, ugyanannyit kell várni, ezért tekinthetjük a csúcsból kimenő élek súlyának a csúcsban töltött időt (A-ból 0, mivel itt nem várakozunk, B-ből nem megyünk tovább...). Így az eredeti gráfon (az élsúlyok beírása után) alkalmazható a Dijkstra algo. | ||
| + | --[[Szerkesztő:Deák Zsolt|Deák Zsolt]] ([[Szerkesztővita:Deák Zsolt|vita]]) 2015. április 8., 12:22 (UTC) | ||
}} | }} | ||
===5. Feladat=== | ===5. Feladat=== | ||
| − | + | Adjacencia-mátrixával adott n csúcsú, élsúlyozott, irányítatlan gráfként ismerjük egy ország úthálózatát (a csomópontok a városok, az élek a közvetlen összeköttetések a városok között). Az élek súlya a városok közti távolságot adja meg. (Feltehetjük, hogy a távolságok egészek.) | |
| + | Adjon egy O(n<sup>6</sup>) lépésszámú algoritmust, ami eldönti, hogy lehetséges-e úgy kiválasztani öt várost, hogy ezektől bármely más város legfeljebb 50 kilométerre van. ''(Ezekbe a városokba lenne érdemes hókoztrókat telepíteni.)'' | ||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
| − | + | *A megoldáshoz először Floyd algoritmussal páronként meghatározzuk az összes város távolságát, ez O(n<sup>3</sup>).<br> | |
| − | + | *A város irányítatlan gráfként van megadva, de ezen könnyen segíthetünk úgy, hogy a jelenlegi élek helyett felveszünk két irányítottat, azonos súllyal. Ez O(n<sup>2</sup>).<br> | |
| + | *Ezek után brute force módszerrel az összes csúcsötösre ellenőrizzük, hogy azok öten lefedik-e (legfeljebb 50 km-re vannak) az összes várost.<br> | ||
| + | **n<sup>5</sup> városötös van, mindegyikre le kell ellenőrizni, hogy jók-e. Az ellenőrzés során végignézzük, az összes csúcsra (n db.), hogy el lehet-e érni. Ez tehát O(n<sup>5</sup>*n)=O(n<sup>6</sup>).<br> | ||
| + | *Összességében ezért O(n<sup>6</sup>) lépésszámú az algoritmus. | ||
}} | }} | ||
| − | ===6. Feladat=== | + | ===6. Feladat (Van megoldás)=== |
| − | + | Egy tömbben adott <math>n</math> darab 0-tól különböző egész szám (lehetnek negatívak is köztük) és adott egy <math>k</math> egész szám is. Adjon <math>O(n \cdot logn)</math> lépésszámú algoritmust, ami eldönti, hogy melyik az a <math>k</math> elem a tömbben, melyek szorzata maximális. | |
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
| − | + | *Első lépésben csökkenő sorrendbe rendezzük az elemeket azok '''abszolút értéke''' szerint. <math> (O(n \cdot logn) </math> pl. összefésüléses rendezéssel. <math>)</math> | |
| + | *Vesszük az első <math>k</math> szám szorzatát. | ||
| + | **Ha ez pozitív, akkor jók vagyunk, nincs más dolgunk. [[File:algel_zh_2013tavasz_6_1.PNG|250px]] | ||
| + | **Ha ez negatív, akkor kiválasztjuk a listából a legkisebb pozitív <math>(A^+)</math> és negatív <math>(A^-)</math> elemet, a maradék listából pedig a legnagyobb pozitív <math>(B^+)</math> és negatív <math>(B^-)</math> elemet. Most meg kell nézni, hogy mit éri meg lecserélni? A pozitívat negatívra, vagy a negatívat pozitívra? | ||
| + | ***Ha <math> (A^- \cdot B^-) < (A^+ \cdot B^+) </math>, akkor a listából kivesszük <math> A^- </math>-t, és berakjuk <math> B^+ </math>-t | ||
| + | ***Ha <math> (A^+ \cdot B^+) < (A^- \cdot B^-) </math>, akkor a listából kivesszük <math> A^+ </math>-t, és berakjuk <math> B^- </math>-t<br>[[File:algel_zh_2013tavasz_6_2.PNG|500px]] | ||
| + | ***Ha nincs a listában pozitív szám, akkor kivesszük a <math>A^-</math>-t, és berakjuk <math>B^+</math>-t<br>[[File:algel_zh_2013tavasz_6_3.PNG|500px]] | ||
| + | ***Ha nincs az egész listában pozitív szám, akkor a legnagyobb számot akkor kapjuk, ha a <math>k</math> darab utolsó elemet vesszük be.<br>[[File:algel_zh_2013tavasz_6_4.PNG|500px]] | ||
| + | |||
}} | }} | ||
| − | ===7. Feladat=== | + | ===7. Feladat (Van megoldás)=== |
| − | + | Az <math>A[1 \dots 2013]</math> tömbben egy kupac adatstruktúrát tárolunk, minden tárolt elem különböző. Tudjuk, hogy ebben a kupacban a legnagyobb elem <math> A[i]</math>. Határozza meg <math> i </math> összes lehetséges értékét! | |
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
| − | + | *Kupac egyik jó tulajdonsága, hogy teljes bináris fa, így az elem számból kiszámolható, hogy milyen magas a fa. | |
| + | **Tudjuk, hogy :<math> 2^{m-1} \leq n \leq 2^{m}-1</math>. | ||
| + | **Ebben az esetben <math> 2^{m-1} \leq 2013 \leq 2^{m}-1 \Rightarrow m = 11</math>. | ||
| + | *A legnagyobb elem vagy a legalsó szinten van, vagy ha az nem "telített", akkor az előtte lévő szinten olyan csúcsok is szóba jöhetnek, akiknek nincsen gyereke. | ||
| + | **Mivel tudjuk, hogy a fa magassága 11, ezért: | ||
| + | ***A kupacban összesen 2047 elemnek van hely, tehát még 34 elem férne el. Ebből pedig az következik, hogy a 10. szinten 17 olyan csúcs van, aminek nincsen fia, így ők még játszhatnak a legnehezebb elem díjáért. | ||
| + | ***A 11. szinten 1024 elem férne el, de tudjuk, hogy hiányzik 34, tehát a 11. szinten csak 990 elem van, amik a legnehezebbek lehetnek a fában. | ||
| + | *Ha a kupacot tömbbe írjuk, akkor azt fentről-lefele, balról-jobbra töltjük fel. | ||
| + | **Az előzőek alapján tudjuk, hogy a 11. szinten 990, a 10. szinten pedig 17 csúcs jöhet szóba, így összesen 1007 helyen lehet a legnehezebb elem. A tömbös elrendezés alapján ez azt jelenti, hogy az <math> i \geq (2013-1007+1) \Rightarrow i \geq 1007</math>. | ||
| + | {{Rejtett | ||
| + | |mutatott=<big>''Avagy...''</big> | ||
| + | |szöveg= | ||
| + | *Avagy bebizonyítható, hogy a legnagyobb elem az az utolsó <math> \left \lceil \frac{n}{2} \right \rceil </math> helyen állhat. | ||
| + | |||
| + | }} | ||
| + | |||
}} | }} | ||
| − | ===8. Feladat=== | + | ===8. Feladat (Van megoldás)=== |
| − | + | '''(a)''' Igaz-e, hogy egy piros-fekete fa tetszőleges belső fekete csúcshoz tartozó részfa (az a részfa, aminek ez a fekete csúcs a gyökere) is egy piros-fekete fa? | |
| + | |||
| + | '''(b)''' Igaz-e ugyanez egy tetszőleges belső piros csúcshoz tartozó részfára? | ||
| + | |||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
| − | + | {{Rejtett | |
| + | |mutatott=<big>''Megjegyzések a feladathoz''</big> | ||
| + | |szöveg= | ||
| + | |||
| + | *Avagy mitől is piros-fekete egy piros-fekete fa? | ||
| + | #Minden nem levél csúcsnak 2 fia van. | ||
| + | #Elemeket belső csúcsban tárolunk. | ||
| + | #teljesül a keresőfa tulajdonság. | ||
| + | #A fa minden csúcsa piros, vagy fekete. | ||
| + | #A gyökér fekete. | ||
| + | #A levelek feketék. | ||
| + | #Minden piros csúcs mindkét gyereke fekete. | ||
| + | #Minden ''v'' csúcsra igaz, hogy az összes ''v''-ből levélbe vezető úton ugyanannyi fekete csúcs van (~fekete magasság). | ||
| + | }} | ||
| + | '''a)''' Igaz-e, hogy egy piros-fekete fa tetszőleges belső fekete csúcshoz tartozó részfa (az a részfa, aminek ez a fekete csúcs a gyökere) is egy piros-fekete fa? | ||
| + | |||
| + | *Igaz. ''(Nem tudom, mennyi magyarázatot, vagy milyen indoklást várnak ide, de a piros-fekete tulajdonságai közül talán csak a fekete magasság szorul magyarázatra (...), a többi elég triviális.)'' | ||
| + | **Ha a részgráfra nem állna fenn a fekete magasság kritériuma, akkor pláne nem fog a teljes gráfra teljesülni, hiszen hiába jó a fekete magasság a pontig, ha a pont tönkre teszi azt :/. | ||
| + | |||
| + | |||
| + | '''b)''' Igaz-e ugyanez egy tetszőleges belső piros csúcshoz tartozó részfára? | ||
| + | *Nem. A gyökérnek feketének kell lennie. | ||
}} | }} | ||
| + | |||
| + | [[Kategória:Infoalap]] | ||
A lap jelenlegi, 2015. április 8., 12:22-kori változata
Tartalomjegyzék
2013.04.03. ZH megoldásai
1. Feladat (Van megoldás)
Mi az a legkisebb r racionális szám, melyre teljesül, hogy [math]\sqrt{1} + \sqrt{2} + \sqrt{3} + ...+\sqrt{n} = O(n^{r}) ?[/math]
- Először megpróbáljuk felülről becsülni:
- Felülről becsüljük a sorozatot, ha az elemeket rendre [math]\sqrt{n}[/math]-nek tekintjük, vagyis:
- [math]\sqrt{n} + \sqrt{n} + \sqrt{n} + ...+\sqrt{n}=n\cdot\sqrt{n}=n^{1.5}=O(n^{1.5}) \Rightarrow r=1.5[/math]
- Felülről becsüljük a sorozatot, ha az elemeket rendre [math]\sqrt{n}[/math]-nek tekintjük, vagyis:
- Most pedig megpróbáljuk alulról becsülni:
- Alulról becsüljük a sorozatot:
- [math] \frac{n}{2 } \cdot \sqrt{1}+\frac{n}{2} \cdot \sqrt{n} \leq \sqrt{1} + \sqrt{2} + \sqrt{3} \dots \sqrt{n} [/math]
- [math] \frac{n}{2 } \cdot \sqrt{1}+\frac{n}{2} \cdot \sqrt{n} = O(n^{1.5}) \Rightarrow r=1.5. [/math]
- Alulról becsüljük a sorozatot:
- A kettőt együttvéve látszik, hogy [math] r = 1.5 .[/math]
2. Feladat (Van megoldás)
Egy [math] A[i,j] [/math] [math]n[/math] x [math]n[/math]-es táblázat minden mezőjében egy egész szám van írva (nem feltétlenül csak pozitívak). Adjon [math] O(n^2) [/math] lépésszámú algoritmust, ami eldönti, hogy melyik az a téglalap alakú része a táblázatnak, melynek bal felső sarka egybe esik a nagy táblázat bal felső sarkával és benne az elemek összege az egyik legnagyobb.
(Vagyis olyan [math]k, l[/math]-t keresünk, amire [math] \sum_{i \leq k, j \leq l}A[i,j] [/math] maximális.)
- Ahogy az többször is segít, úgy most is, hogy felrajzolunk magunknak egy 3x3, vagy 4x4-es táblázatot, és nézegetjük, hogyan kéne dolgozni...
- A feladatban 1-1 lépésnek vettem:
- 1 művelet ([math] +,- [/math]) elvégzését (vagyis a [math] B[i,j]=B[i-1,j]+B[i,j-1]+A[i,j]-B[i-1,j-1] [/math] 3 lépés).
- 1 értéke beírása a cellába.
- 1 összehasonlítás (és esetleges cserék).
3. Feladat (Van megoldás)
Kaphatjuk-e az 1,7,3,6,11,15,22,17,14,12,9 számsorozatot úgy, hogy egy (a szokásos rendezést használó) bináris keresőfában tárolt elemeket posztorder sorrendben kiolvasunk?
- Szokásos rendezést használó bináris keresőfa: [math]bal(x) \lt x \lt jobb(x)[/math]
- Postorder:
- Rekurzívan [math] bal(x) \rightarrow jobb(x) \rightarrow x [/math].(Magyarul: előbb meglátogatja a gyökérnél kisebbeket, utána a nagyobbakat, és ezután jön csak a gyökér.)
- Egyik fontos tulajdonsága, hogy a gyökér az mindig a (figyelt) lista végén van.
- Az 1. sorban a 9 lesz a gyökér. Felrajzoljuk a 9-t gyökérnek. (Bal oldalt lesz a hiba, de gyakorlásképp nézzük inkább a jobb oldalt.)
- A 2. sorban a 12 lesz a gyökér, így a 12-est felrajzoljuk a 9-es jobb fiának. Nála csak a 11 a kisebb (a vizsgált listában), így a 11-t berajzoljuk a 12 bal fiának.
- A 3. sorban 14 lesz a gyökér, így a 14-est felrajzoljuk a 12-es jobb fiának.
- A 4. sorban a 17 lesz a gyökér, így ez a 14-es jobb fia lesz. A 15 és 22 pedig értelemszerűen a bal, és jobb fia lesz 17-nek.
- Az 5. sorban a gyökér a 6 lesz, így azt berajzoljuk a 9-es bal fiának. És itt látszik is, hogy hiba van, hiszen [math] \lt \gt \lt [/math] sorrend van, ebből következik, hogy ilyen fa nem létezhet.
4. Feladat (Van megoldás)
Adjacencia-mátrixával adott [math]n[/math] csúcsú, irányított gráfként ismerjük egy város úthálózatát. El szeretnék jutni [math]A[/math] pontból [math]B[/math] pontba, de sajnos minden csomóponthoz várnunk kell a nagy hóesés miatt, a várakozás hossza minden csomópontra ismert és független attól, hogy merre akarunk továbbmenni. Adjon algoritmust, ami [math]O(n^2)[/math] lépésben eldönti, hogy merre menjünk, hogy a lehető legkevesebbet kelljen várni összességében. (A csomópontok közötti utak hosszának megtétele a várakozáshoz képest elhanyagolható időbe telik, tekintsük 0-nak. [math]A[/math]-ban és [math]B[/math]-ben nem kell várakozni.)
- A "probléma", hogy a csúcsoknak van súlya (ill. az éleknek is van, de az 0), amivel nem igen tudunk mit kezdeni. De nem hiába volt BSZ1 (vagy BSZ2?), ahol megtanultuk, hogy könnyedén csinálhatunk a csúcssúlyból élsúlyt.
- Az adott pontot (X) lecseréljük 2 pontra (X1, X2). Ami eddig X-be ment, az menjen X1-be, és ami X-ből ment, az menjen X2-ből. (Vagyis X1-ből csak X2-be megy él, és X2-be csak az X1 megy.)
- A 2 pontot összekötjük, a köztük menő élsúly pedig az X pont súlya lesz.
- Csináljuk hát ezt ezzel a gráffal:
- Az eredeti [math] n [/math] csúcsú G gráfból csinálunk így egy F gráfot, melyben [math] 2n [/math] csúcs lesz (és az élszám is n-nel nő, de ez most minket annyira nem izgat).
- Ebben az F gráfban kell megtalálni a legrövidebb utat egy "X2"-ből egy "Y1"-be.
- A Dijkstra-algoritmus [math] O(n^2) [/math] lépésben keres legrövidebb utat, ebben az esetben [math] O((2n)^2)=4O(n^2)=O(n^2)[/math].
- Így a feladat ezzel meg is oldva.
Talán egyszerűbben: mivel 0 az utazási idő (élsúlyok) és bármerre megyünk egy csúcsból, ugyanannyit kell várni, ezért tekinthetjük a csúcsból kimenő élek súlyának a csúcsban töltött időt (A-ból 0, mivel itt nem várakozunk, B-ből nem megyünk tovább...). Így az eredeti gráfon (az élsúlyok beírása után) alkalmazható a Dijkstra algo.
--Deák Zsolt (vita) 2015. április 8., 12:22 (UTC)5. Feladat
Adjacencia-mátrixával adott n csúcsú, élsúlyozott, irányítatlan gráfként ismerjük egy ország úthálózatát (a csomópontok a városok, az élek a közvetlen összeköttetések a városok között). Az élek súlya a városok közti távolságot adja meg. (Feltehetjük, hogy a távolságok egészek.) Adjon egy O(n6) lépésszámú algoritmust, ami eldönti, hogy lehetséges-e úgy kiválasztani öt várost, hogy ezektől bármely más város legfeljebb 50 kilométerre van. (Ezekbe a városokba lenne érdemes hókoztrókat telepíteni.)
- A megoldáshoz először Floyd algoritmussal páronként meghatározzuk az összes város távolságát, ez O(n3).
- A város irányítatlan gráfként van megadva, de ezen könnyen segíthetünk úgy, hogy a jelenlegi élek helyett felveszünk két irányítottat, azonos súllyal. Ez O(n2).
- Ezek után brute force módszerrel az összes csúcsötösre ellenőrizzük, hogy azok öten lefedik-e (legfeljebb 50 km-re vannak) az összes várost.
- n5 városötös van, mindegyikre le kell ellenőrizni, hogy jók-e. Az ellenőrzés során végignézzük, az összes csúcsra (n db.), hogy el lehet-e érni. Ez tehát O(n5*n)=O(n6).
- n5 városötös van, mindegyikre le kell ellenőrizni, hogy jók-e. Az ellenőrzés során végignézzük, az összes csúcsra (n db.), hogy el lehet-e érni. Ez tehát O(n5*n)=O(n6).
- Összességében ezért O(n6) lépésszámú az algoritmus.
6. Feladat (Van megoldás)
Egy tömbben adott [math]n[/math] darab 0-tól különböző egész szám (lehetnek negatívak is köztük) és adott egy [math]k[/math] egész szám is. Adjon [math]O(n \cdot logn)[/math] lépésszámú algoritmust, ami eldönti, hogy melyik az a [math]k[/math] elem a tömbben, melyek szorzata maximális.
- Első lépésben csökkenő sorrendbe rendezzük az elemeket azok abszolút értéke szerint. [math] (O(n \cdot logn) [/math] pl. összefésüléses rendezéssel. [math])[/math]
- Vesszük az első [math]k[/math] szám szorzatát.
- Ha ez pozitív, akkor jók vagyunk, nincs más dolgunk.
- Ha ez negatív, akkor kiválasztjuk a listából a legkisebb pozitív [math](A^+)[/math] és negatív [math](A^-)[/math] elemet, a maradék listából pedig a legnagyobb pozitív [math](B^+)[/math] és negatív [math](B^-)[/math] elemet. Most meg kell nézni, hogy mit éri meg lecserélni? A pozitívat negatívra, vagy a negatívat pozitívra?
- Ha [math] (A^- \cdot B^-) \lt (A^+ \cdot B^+) [/math], akkor a listából kivesszük [math] A^- [/math]-t, és berakjuk [math] B^+ [/math]-t
- Ha [math] (A^+ \cdot B^+) \lt (A^- \cdot B^-) [/math], akkor a listából kivesszük [math] A^+ [/math]-t, és berakjuk [math] B^- [/math]-t
- Ha nincs a listában pozitív szám, akkor kivesszük a [math]A^-[/math]-t, és berakjuk [math]B^+[/math]-t
- Ha nincs az egész listában pozitív szám, akkor a legnagyobb számot akkor kapjuk, ha a [math]k[/math] darab utolsó elemet vesszük be.
- Ha ez pozitív, akkor jók vagyunk, nincs más dolgunk.
7. Feladat (Van megoldás)
Az [math]A[1 \dots 2013][/math] tömbben egy kupac adatstruktúrát tárolunk, minden tárolt elem különböző. Tudjuk, hogy ebben a kupacban a legnagyobb elem [math] A[i][/math]. Határozza meg [math] i [/math] összes lehetséges értékét!
- Kupac egyik jó tulajdonsága, hogy teljes bináris fa, így az elem számból kiszámolható, hogy milyen magas a fa.
- Tudjuk, hogy :[math] 2^{m-1} \leq n \leq 2^{m}-1[/math].
- Ebben az esetben [math] 2^{m-1} \leq 2013 \leq 2^{m}-1 \Rightarrow m = 11[/math].
- A legnagyobb elem vagy a legalsó szinten van, vagy ha az nem "telített", akkor az előtte lévő szinten olyan csúcsok is szóba jöhetnek, akiknek nincsen gyereke.
- Mivel tudjuk, hogy a fa magassága 11, ezért:
- A kupacban összesen 2047 elemnek van hely, tehát még 34 elem férne el. Ebből pedig az következik, hogy a 10. szinten 17 olyan csúcs van, aminek nincsen fia, így ők még játszhatnak a legnehezebb elem díjáért.
- A 11. szinten 1024 elem férne el, de tudjuk, hogy hiányzik 34, tehát a 11. szinten csak 990 elem van, amik a legnehezebbek lehetnek a fában.
- Mivel tudjuk, hogy a fa magassága 11, ezért:
- Ha a kupacot tömbbe írjuk, akkor azt fentről-lefele, balról-jobbra töltjük fel.
- Az előzőek alapján tudjuk, hogy a 11. szinten 990, a 10. szinten pedig 17 csúcs jöhet szóba, így összesen 1007 helyen lehet a legnehezebb elem. A tömbös elrendezés alapján ez azt jelenti, hogy az [math] i \geq (2013-1007+1) \Rightarrow i \geq 1007[/math].
- Avagy bebizonyítható, hogy a legnagyobb elem az az utolsó [math] \left \lceil \frac{n}{2} \right \rceil [/math] helyen állhat.
8. Feladat (Van megoldás)
(a) Igaz-e, hogy egy piros-fekete fa tetszőleges belső fekete csúcshoz tartozó részfa (az a részfa, aminek ez a fekete csúcs a gyökere) is egy piros-fekete fa?
(b) Igaz-e ugyanez egy tetszőleges belső piros csúcshoz tartozó részfára?
- Avagy mitől is piros-fekete egy piros-fekete fa?
- Minden nem levél csúcsnak 2 fia van.
- Elemeket belső csúcsban tárolunk.
- teljesül a keresőfa tulajdonság.
- A fa minden csúcsa piros, vagy fekete.
- A gyökér fekete.
- A levelek feketék.
- Minden piros csúcs mindkét gyereke fekete.
- Minden v csúcsra igaz, hogy az összes v-ből levélbe vezető úton ugyanannyi fekete csúcs van (~fekete magasság).
a) Igaz-e, hogy egy piros-fekete fa tetszőleges belső fekete csúcshoz tartozó részfa (az a részfa, aminek ez a fekete csúcs a gyökere) is egy piros-fekete fa?
- Igaz. (Nem tudom, mennyi magyarázatot, vagy milyen indoklást várnak ide, de a piros-fekete tulajdonságai közül talán csak a fekete magasság szorul magyarázatra (...), a többi elég triviális.)
- Ha a részgráfra nem állna fenn a fekete magasság kritériuma, akkor pláne nem fog a teljes gráfra teljesülni, hiszen hiába jó a fekete magasság a pontig, ha a pont tönkre teszi azt :/.
b) Igaz-e ugyanez egy tetszőleges belső piros csúcshoz tartozó részfára?
- Nem. A gyökérnek feketének kell lennie.