„Algoritmuselmélet - Vizsga, 2013.05.30.” változatai közötti eltérés
| (13 közbenső módosítás, amit 4 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| + | {{Vissza|Algoritmuselmélet}} | ||
| + | |||
==2013.06.06. vizsga megoldásai== | ==2013.06.06. vizsga megoldásai== | ||
===1. Feladat=== | ===1. Feladat=== | ||
| − | + | Ebben a feladatban a Floyd algoritmussal kapcsolatos kérdésekre kell válaszolnia. (A Floyd-algoritmus egy grában minden pontpárra meghatározza a köztük levő legrövidebb út hosszát.) | |
| + | |||
| + | '''(a)''' Mit jelöl az <math> F_k </math> mátrix <math> F_k[i,j] </math> eleme? | ||
| + | |||
| + | '''(b)''' Hogyan kell kiszámolni az <math> F_{k-1} </math> mátrixból az <math> F_k </math> mátrixot? | ||
| + | |||
| + | '''(c)''' Igazolja, hogy ez a kiszámítási mód helyes! | ||
| + | |||
| + | '''(d)''' Mennyi a lépésszáma a '''(b)''' lépés egyszeri végrehajtásának? (A lépésszámot nem kell igazolni.) | ||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
| − | + | '''a)''' <math> F_k[i,j] </math> azon <math> i \rightarrow j </math> utak legrövidebbjeinek a hosszát tartalmazza, amelyek közbülső pontjai <math>k</math>-nál nem nagyobb sorszámúak. ''(Magyarul: Az <math> F_k[i,j] </math> azt mondja meg, hogy <math>i</math>-ből <math>j</math>-be mennyi a legrövidebb út összsúlya, ha csak az első <math>k</math> darab csúcsot használtuk.)'' | |
| + | |||
| + | '''b)''' <math> F_k[i,j]:=min\left \{ F_{k-1}[i,k]+F_{k-1}[k,j],F_{k-1}[i,j]\right \} </math> ''<math>(</math>Vagyis vagy az <math> i \rightarrow k \rightarrow j </math> lesz a legrövidebb út, vagy "marad a régi" <math> i \rightarrow j .)</math>'' | ||
| + | |||
| + | '''c)''' Tulajdonképpen az előzőből következik. Hiszen vagy nem változik az új csúccsal a legrövidebb út a 2 pont között <math> (i \rightarrow j) </math>, vagy ha igen, akkor az a <math> (i \rightarrow k) + (k \rightarrow j) </math> lesz az. | ||
| + | |||
| + | '''d)''' <math> O(n^2) </math>. ''<math>(</math>Maga az algoritmus <math>O(n^3)</math>, de csúcsonként <math> O(n^2) </math>, vagyis <math> n \cdot O(n^2) = O(n^3) ).</math>'' | ||
}} | }} | ||
| 20. sor: | 36. sor: | ||
*Minden belső csúcsnak 2, vagy 3 fia lehet, se több, se kevesebb. ''(Kivéve, ha csak 1 elemet tárolunk a fában, mert akkor a gyökérnek csak 1 fia van.)'' | *Minden belső csúcsnak 2, vagy 3 fia lehet, se több, se kevesebb. ''(Kivéve, ha csak 1 elemet tárolunk a fában, mert akkor a gyökérnek csak 1 fia van.)'' | ||
*A fa levelei a gyökértől egyenlő távolságra vannak (vagyis a levelek 1 szinten vannak). | *A fa levelei a gyökértől egyenlő távolságra vannak (vagyis a levelek 1 szinten vannak). | ||
| − | *A belső csúcsokban mutatókat (M) és 1, vagy 2 | + | *A belső csúcsokban mutatókat (M) és 1, vagy 2 kulcsot (S) tárolunk. |
| − | **Ha a csúcsnak 2 fia van, akkor 2 mutatót, és egy | + | **Ha a csúcsnak 2 fia van, akkor 2 mutatót, és egy kulcsot tárol. [[File:Algel vizsga 2013tavasz V1 2 2fia.png|300px]] |
***A bal részfában az elemek kisebbek, mint S1. | ***A bal részfában az elemek kisebbek, mint S1. | ||
***A jobb részfában az elemek nagyobb-egyenlőek, mint S1 (vagyis az 1. elem S1). | ***A jobb részfában az elemek nagyobb-egyenlőek, mint S1 (vagyis az 1. elem S1). | ||
| − | **Ha a csúcsnak 3 fia van, akkor 3 mutatót, és 2 | + | **Ha a csúcsnak 3 fia van, akkor 3 mutatót, és 2 kulcsot tárol. [[File:Algel_vizsga_2013tavasz_V1_2_3fia.png|400px]] |
***A bal részfában az elemek kisebbek, mint S1. | ***A bal részfában az elemek kisebbek, mint S1. | ||
***A középső részfában az elemek nagyobb-egyenlőek, mint S1 (vagyis az 1. elem S1), de kisebbek, mint S2. | ***A középső részfában az elemek nagyobb-egyenlőek, mint S1 (vagyis az 1. elem S1), de kisebbek, mint S2. | ||
***A jobb részfában az elemek nagyobb-egyenlőek, mint S2 (vagyis az 1. elem S2). | ***A jobb részfában az elemek nagyobb-egyenlőek, mint S2 (vagyis az 1. elem S2). | ||
| − | |||
'''Adjon felső becslést a fa szintszámára n tárolt elem esetén, állítását bizonyítsa is!''' | '''Adjon felső becslést a fa szintszámára n tárolt elem esetén, állítását bizonyítsa is!''' | ||
<math>log_2n+1\leq m \leq log_3n+1</math>, ahol <math>m</math> a fa szintszáma. | <math>log_2n+1\leq m \leq log_3n+1</math>, ahol <math>m</math> a fa szintszáma. | ||
| + | |||
| + | $$$ Ez nem pont fordítva van a dián? $$$ | ||
''Bizonyítás:'' | ''Bizonyítás:'' | ||
| 50. sor: | 67. sor: | ||
}} | }} | ||
| − | ===4. Feladat=== | + | ===4. Feladat (Van megoldás)=== |
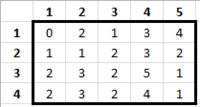
| − | + | Van egy tábla <math> (n</math> <big>x</big> <math>m</math> kockákból álló<math> ) </math>. Az <math> A </math> <math> n</math> <big>x</big> <math>m</math>-es mátrixban adott, hogy az egyes kockákban hány mogyoró van (a mogyorók nem lógnak át egyik kockából a másikba). Két gyerek akar osztozkodni a csokin, úgy, hogy a csokit kéfelé törik (egyenes vonal mentén, párhuzamosan a tábla valamelyik szélével). Egy osztkozkodás igazságtalansági faktorát a következőképpen kaphatjuk: ha az egyik darabban <math> k_1 </math> kocka csoki, és <math> m_1 </math> darab mogyoró van, a másikban pedig <math> k_2 </math> kocka csoki és <math> m_2 </math> darab mogyoró, akkor az igazságtalansági faktor <math> \left | \left ( k_1+m_1 \right ) -(k_2+m_2)\right | </math>. Adjon <math> O(nm) </math> lépést használó algoritmust, ami eldönti, hogy melyik szétosztásnak a legkisebb az igazságtalansági faktora. (Egy lépésnek számít, ha kiolvasunk egy értéket az <math> A </math> mátrixból vagy ha összeadást, illetve kivonást hajtunk végre két számon.) | |
| + | |||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
| + | [[File:algel_vizsga1_2013tavasz_4_csoki.PNG|200px]] | ||
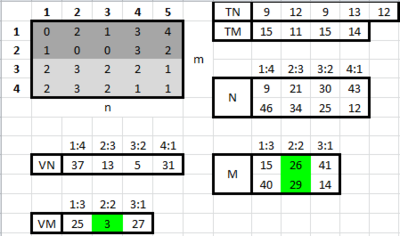
| + | *Hozzunk létre egy <math> n </math> elemű <math> TN </math> tömböt, ahol az <math> i. </math> cellában az szerepel, hogy az <math> A </math> mátrix annyiadik oszlopában mennyi a <math> k+m </math>. ''(ez <math> n*m </math> kiolvasás, és <math> n*(m-1) </math> összeadás, vagyis <math> \Rightarrow O(nm) </math>. | ||
| + | *Hozzunk létre egy <math> m </math> elemű <math> TM </math> tömböt, ahol az <math> i. </math> cellában az szerepel, hogy az <math> A </math> mátrix annyiadik sorában mennyi a <math> k+m </math>. ''(ez <math> m*n </math> kiolvasás, és <math> m*(n-1) </math> összeadás, vagyis <math> \Rightarrow O(nm) </math>. | ||
| + | [[File:algel_vizsga1_2013tavasz_4_tn_tm.PNG|200px]] | ||
| + | *Hozzunk létre egy <math> (n-1) </math> x <math> 2 </math>-es <math> N </math> tömböt, ahol az 1. sorban balról jobbra nézzük, mennyi a <math> k+m </math>, a 2. sorban pedig jobbról balra. ''<math>(</math>1. sor a <math> (k_1+m_1) </math>, 2. sor pedig a hozzá tartozó <math> (k_2+m_2) .)</math> | ||
| + | **<math>N[1,1]= TN[1] </math> majd <math>N[i,1]= N[i-1,1]+TN[i] , i=2...(n-1)</math>. | ||
| + | **<math>N[1,2]= \sum_{i=2}^{n}TN[i] </math> majd <math>N[i,2]= N[i-1,2]-TN[i] , i=2...(n-1)</math>. | ||
| + | *Hozzunk létre egy <math> (m-1) </math> x <math> 2 </math>-es <math> M </math> tömböt, ahol az 1. sorban fentről lefele nézzük, mennyi a <math> k+m </math>, a 2. sorban pedig alulról felfele. ''<math>(</math>1. sor a <math> (k_1+m_1) </math>, 2. sor pedig a hozzá tartozó <math> (k_2+m_2) .)</math> | ||
| + | **<math>M[1,1]= TM[1] </math> majd <math>M[i,1]= M[i-1,1]+TM[i] , i=2...(m-1)</math>. | ||
| + | **<math>M[1,2]= \sum_{i=2}^{m}TM[i] </math> majd <math>M[i,2]= M[i-1,2]-TM[i] , i=2...(m-1)</math>. | ||
| + | [[File:algel_vizsga1_2013tavasz_4_N_M.PNG|200px]] | ||
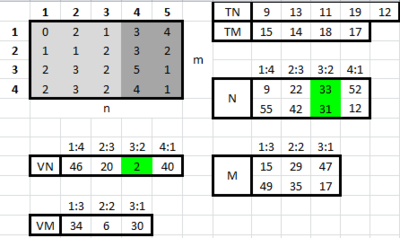
| + | *Az <math> N </math> és <math> M </math> tömbök létrehozása <math> O(n) </math> és <math> O(m) </math> lépést igényel. | ||
| + | *Nincs is más dolgunk, mint végigmenni az <math> N </math> és <math> M </math> tömbökön úgy, hogy az <math> i. </math> oszlopban vesszük a 2 szám különbségének abszolút értékét, vagyis az igazságtalansági faktort számoljuk, és mindig elmentjük egy változóba a minimumot, és a ehhez tartozó törésvonalat. Ez is <math> O(n) </math> és <math> O(m) </math> lépés. | ||
| + | *Összesen tehát <math> O(nm)+O(nm)+O(n)+O(m)+O(n)+O(m)=O(nm) </math> lépéssel megoldottuk a feladatot. | ||
| + | :::::[[File:algel_vizsga1_2013tavasz_4_1.PNG|400px]] [[File:algel_vizsga1_2013tavasz_4_2.PNG|400px]] | ||
| − | |||
}} | }} | ||
| 72. sor: | 104. sor: | ||
<math>\sum_{i=0}^{k} r^i = \frac{1-r^{k+1}} {1-r} </math>, ahol <math> k = \left \lfloor log_4n \right \rfloor, r = \frac{1}{16}</math>, vagyis <math>\frac{1-\frac{1}{16}^{\left \lfloor log_4n \right \rfloor+1}} {1-\frac{1}{16}}</math><br> | <math>\sum_{i=0}^{k} r^i = \frac{1-r^{k+1}} {1-r} </math>, ahol <math> k = \left \lfloor log_4n \right \rfloor, r = \frac{1}{16}</math>, vagyis <math>\frac{1-\frac{1}{16}^{\left \lfloor log_4n \right \rfloor+1}} {1-\frac{1}{16}}</math><br> | ||
| − | <math>\frac{1-\frac{1}{16}^{\left \lfloor log_4n \right \rfloor+1}} {1-\frac{1}{16}} < 2 ,</math><big>ha</big> <math> n \geq 1</math> | + | <math>\frac{1-\frac{1}{16}^{\left \lfloor log_4n \right \rfloor+1}} {1-\frac{1}{16}} < 2 ,</math><big>ha</big> <math> n \geq 1</math> ''(A lényeg, hogy felülről becsüljük!)'' |
| − | Tehát <math> T(n)= | + | Tehát <math> T(n) = \dots \leq 1+2 \cdot cn^2=O(n^2)</math> |
}} | }} | ||
| − | ===6. Feladat=== | + | ===6. Feladat (Van megoldás)=== |
Egy ország ''n'' kis szigetből áll. Szeretnénk néhány hajójáratot indítani a szigetek között úgy, hogy bárhonnan bárhova el lehessen jutni (esetleg átszállással). Ehhez ismerjük bármely két szigetre, hogy mennyibe kerül egy évben a hajójárat fenntartása közöttük, illetve azt, hogy mekkora az itt várható éves bevétel. Adjon algoritmust, ami ezen adatok ismeretében <math>O(n^2)</math> időben meghatározza, hogy hol indítsuk el a hajójáratokat, ha a lehető legnagyobb várható éves hasznot (vagy a lehető legkisebb veszteséget) szeretnénk elérni. (Egy szigeten egy hajóállomás van csak). | Egy ország ''n'' kis szigetből áll. Szeretnénk néhány hajójáratot indítani a szigetek között úgy, hogy bárhonnan bárhova el lehessen jutni (esetleg átszállással). Ehhez ismerjük bármely két szigetre, hogy mennyibe kerül egy évben a hajójárat fenntartása közöttük, illetve azt, hogy mekkora az itt várható éves bevétel. Adjon algoritmust, ami ezen adatok ismeretében <math>O(n^2)</math> időben meghatározza, hogy hol indítsuk el a hajójáratokat, ha a lehető legnagyobb várható éves hasznot (vagy a lehető legkisebb veszteséget) szeretnénk elérni. (Egy szigeten egy hajóállomás van csak). | ||
{{Rejtett | {{Rejtett | ||
| 84. sor: | 116. sor: | ||
|szöveg= | |szöveg= | ||
| − | + | *Első lépésben az élsúly legyen a <math> Profit = -(Bevetel - Kiadas) .</math> | |
| + | *Vegyük fel az összes profitot termelő, vagy legalábbis veszteséget nem termelő éleket <math> (Profit \geq 0 )</math> <math> \Rightarrow O(n^2) </math> lépés. Ez legyen mondjuk a G gráf. | ||
| + | *Két eshetőség áll fenn: | ||
| + | **Ha a G gráf összefüggő, akkor jók is vagyunk, nincs további teendőnk, meg is vagyunk. | ||
| + | **Ha nem összefüggő, akkor: | ||
| + | ***Az egyes komponenseket tekintsük egy pontnak. Minden olyan él, ami ebbe a komponensbe megy, menjen ebbe a pontba. Így kapunk egy F gráfot. | ||
| + | ***Erre az F gráfra hívunk meg egy Prim-algoritmust, ami <math> O(n^2) </math> időben keres az F gráfban egy minimális feszítőfát ''(vagyis a komponenseket - ami most jelenleg 1-1 pont a gráfban - a lehető legkisebb költségű élekkel köti össze)''. | ||
| + | |||
| + | *Tehát Prim-algoritmussal, vagy anélkül <math> O(n^2) </math> időben megmondjuk, hogy mely hajójáratok indításával lesz az évi bevétel a legmagasabb. | ||
}} | }} | ||
| 104. sor: | 144. sor: | ||
TODO | TODO | ||
}} | }} | ||
| + | |||
| + | [[Kategória:Infoalap]] | ||
A lap jelenlegi, 2015. június 18., 17:22-kori változata
Tartalomjegyzék
2013.06.06. vizsga megoldásai
1. Feladat
Ebben a feladatban a Floyd algoritmussal kapcsolatos kérdésekre kell válaszolnia. (A Floyd-algoritmus egy grában minden pontpárra meghatározza a köztük levő legrövidebb út hosszát.)
(a) Mit jelöl az [math] F_k [/math] mátrix [math] F_k[i,j] [/math] eleme?
(b) Hogyan kell kiszámolni az [math] F_{k-1} [/math] mátrixból az [math] F_k [/math] mátrixot?
(c) Igazolja, hogy ez a kiszámítási mód helyes!
(d) Mennyi a lépésszáma a (b) lépés egyszeri végrehajtásának? (A lépésszámot nem kell igazolni.)
a) [math] F_k[i,j] [/math] azon [math] i \rightarrow j [/math] utak legrövidebbjeinek a hosszát tartalmazza, amelyek közbülső pontjai [math]k[/math]-nál nem nagyobb sorszámúak. (Magyarul: Az [math] F_k[i,j] [/math] azt mondja meg, hogy [math]i[/math]-ből [math]j[/math]-be mennyi a legrövidebb út összsúlya, ha csak az első [math]k[/math] darab csúcsot használtuk.)
b) [math] F_k[i,j]:=min\left \{ F_{k-1}[i,k]+F_{k-1}[k,j],F_{k-1}[i,j]\right \} [/math] [math]([/math]Vagyis vagy az [math] i \rightarrow k \rightarrow j [/math] lesz a legrövidebb út, vagy "marad a régi" [math] i \rightarrow j .)[/math]
c) Tulajdonképpen az előzőből következik. Hiszen vagy nem változik az új csúccsal a legrövidebb út a 2 pont között [math] (i \rightarrow j) [/math], vagy ha igen, akkor az a [math] (i \rightarrow k) + (k \rightarrow j) [/math] lesz az.
d) [math] O(n^2) [/math]. [math]([/math]Maga az algoritmus [math]O(n^3)[/math], de csúcsonként [math] O(n^2) [/math], vagyis [math] n \cdot O(n^2) = O(n^3) ).[/math]2. Feladat (Van megoldás)
Adja meg a 2-3 fa definícióját! Adjon felső becslést a fa szintszámára n tárolt elem esetén, állítását bizonyítsa is!
Adja meg a 2-3 fa definícióját!
- Elemeket csak a levelekben tárolunk.
- Az elemek balról jobbra növekvő sorrendben állnak.
- Minden belső csúcsnak 2, vagy 3 fia lehet, se több, se kevesebb. (Kivéve, ha csak 1 elemet tárolunk a fában, mert akkor a gyökérnek csak 1 fia van.)
- A fa levelei a gyökértől egyenlő távolságra vannak (vagyis a levelek 1 szinten vannak).
- A belső csúcsokban mutatókat (M) és 1, vagy 2 kulcsot (S) tárolunk.
- Ha a csúcsnak 2 fia van, akkor 2 mutatót, és egy kulcsot tárol.
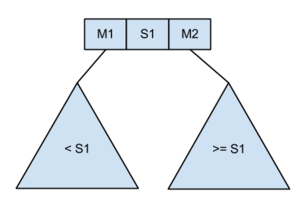
- A bal részfában az elemek kisebbek, mint S1.
- A jobb részfában az elemek nagyobb-egyenlőek, mint S1 (vagyis az 1. elem S1).
- Ha a csúcsnak 3 fia van, akkor 3 mutatót, és 2 kulcsot tárol.
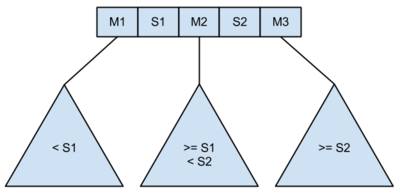
- A bal részfában az elemek kisebbek, mint S1.
- A középső részfában az elemek nagyobb-egyenlőek, mint S1 (vagyis az 1. elem S1), de kisebbek, mint S2.
- A jobb részfában az elemek nagyobb-egyenlőek, mint S2 (vagyis az 1. elem S2).
- Ha a csúcsnak 2 fia van, akkor 2 mutatót, és egy kulcsot tárol.
Adjon felső becslést a fa szintszámára n tárolt elem esetén, állítását bizonyítsa is!
[math]log_2n+1\leq m \leq log_3n+1[/math], ahol [math]m[/math] a fa szintszáma.
$$$ Ez nem pont fordítva van a dián? $$$
Bizonyítás:
- [math]log_2n+1\leq m[/math]
- Minden belső csúcsnak legalább 2 fia van, így az [math]i.[/math] szinten legalább [math]2^{i-1}[/math] csúcs van, tehát: [math]2^{m-1} \geq n \Rightarrow m-1 \geq log_2n \Rightarrow m \geq log_2n+1[/math]
- [math]m\leq log_3n+1[/math]
- Minden belső csúcsnak maximum 3 fia van, így az [math]i.[/math] szinten maximum [math]3^{i-1}[/math] csúcs van, tehát: [math]3^{m-1} \leq n \Rightarrow m-1 \leq log_3n \Rightarrow m \leq log_3n+1[/math]
3. Feladat
TODO
4. Feladat (Van megoldás)
Van egy tábla [math] (n[/math] x [math]m[/math] kockákból álló[math] ) [/math]. Az [math] A [/math] [math] n[/math] x [math]m[/math]-es mátrixban adott, hogy az egyes kockákban hány mogyoró van (a mogyorók nem lógnak át egyik kockából a másikba). Két gyerek akar osztozkodni a csokin, úgy, hogy a csokit kéfelé törik (egyenes vonal mentén, párhuzamosan a tábla valamelyik szélével). Egy osztkozkodás igazságtalansági faktorát a következőképpen kaphatjuk: ha az egyik darabban [math] k_1 [/math] kocka csoki, és [math] m_1 [/math] darab mogyoró van, a másikban pedig [math] k_2 [/math] kocka csoki és [math] m_2 [/math] darab mogyoró, akkor az igazságtalansági faktor [math] \left | \left ( k_1+m_1 \right ) -(k_2+m_2)\right | [/math]. Adjon [math] O(nm) [/math] lépést használó algoritmust, ami eldönti, hogy melyik szétosztásnak a legkisebb az igazságtalansági faktora. (Egy lépésnek számít, ha kiolvasunk egy értéket az [math] A [/math] mátrixból vagy ha összeadást, illetve kivonást hajtunk végre két számon.)
- Hozzunk létre egy [math] n [/math] elemű [math] TN [/math] tömböt, ahol az [math] i. [/math] cellában az szerepel, hogy az [math] A [/math] mátrix annyiadik oszlopában mennyi a [math] k+m [/math]. (ez [math] n*m [/math] kiolvasás, és [math] n*(m-1) [/math] összeadás, vagyis [math] \Rightarrow O(nm) [/math].
- Hozzunk létre egy [math] m [/math] elemű [math] TM [/math] tömböt, ahol az [math] i. [/math] cellában az szerepel, hogy az [math] A [/math] mátrix annyiadik sorában mennyi a [math] k+m [/math]. (ez [math] m*n [/math] kiolvasás, és [math] m*(n-1) [/math] összeadás, vagyis [math] \Rightarrow O(nm) [/math].
- Hozzunk létre egy [math] (n-1) [/math] x [math] 2 [/math]-es [math] N [/math] tömböt, ahol az 1. sorban balról jobbra nézzük, mennyi a [math] k+m [/math], a 2. sorban pedig jobbról balra. [math]([/math]1. sor a [math] (k_1+m_1) [/math], 2. sor pedig a hozzá tartozó [math] (k_2+m_2) .)[/math]
- [math]N[1,1]= TN[1] [/math] majd [math]N[i,1]= N[i-1,1]+TN[i] , i=2...(n-1)[/math].
- [math]N[1,2]= \sum_{i=2}^{n}TN[i] [/math] majd [math]N[i,2]= N[i-1,2]-TN[i] , i=2...(n-1)[/math].
- Hozzunk létre egy [math] (m-1) [/math] x [math] 2 [/math]-es [math] M [/math] tömböt, ahol az 1. sorban fentről lefele nézzük, mennyi a [math] k+m [/math], a 2. sorban pedig alulról felfele. [math]([/math]1. sor a [math] (k_1+m_1) [/math], 2. sor pedig a hozzá tartozó [math] (k_2+m_2) .)[/math]
- [math]M[1,1]= TM[1] [/math] majd [math]M[i,1]= M[i-1,1]+TM[i] , i=2...(m-1)[/math].
- [math]M[1,2]= \sum_{i=2}^{m}TM[i] [/math] majd [math]M[i,2]= M[i-1,2]-TM[i] , i=2...(m-1)[/math].
- Az [math] N [/math] és [math] M [/math] tömbök létrehozása [math] O(n) [/math] és [math] O(m) [/math] lépést igényel.
- Nincs is más dolgunk, mint végigmenni az [math] N [/math] és [math] M [/math] tömbökön úgy, hogy az [math] i. [/math] oszlopban vesszük a 2 szám különbségének abszolút értékét, vagyis az igazságtalansági faktort számoljuk, és mindig elmentjük egy változóba a minimumot, és a ehhez tartozó törésvonalat. Ez is [math] O(n) [/math] és [math] O(m) [/math] lépés.
- Összesen tehát [math] O(nm)+O(nm)+O(n)+O(m)+O(n)+O(m)=O(nm) [/math] lépéssel megoldottuk a feladatot.
5. Feladat (Van megoldás)
Egy algoritmus lépésszámáról tudjuk, hogy [math] T(n) = T\left(\left \lfloor \frac{n}{4} \right \rfloor\right) + O(n^2)[/math] és tudjuk azt is, hogy [math] T(1)=T(2)=T(3)=1[/math]. Bizonyítsa be, hogy [math] T(n)=O(n^2)[/math].
Van olyan [math] c \gt 0[/math] és [math] n_0[/math], hogy [math] n\gt n_0[/math] esetén [math] T(n)=T\left(\left \lfloor \frac{n}{4} \right \rfloor\right)+O(n^2) \leq T\left(\left \lfloor \frac{n}{4} \right \rfloor\right)+cn^2 \leq T\left(\left \lfloor \frac{n}{16} \right \rfloor\right)+c\left(n^2+\left(\frac{n^2}{4^2} \right)\right) \leq T\left(\left \lfloor \frac{n}{64} \right \rfloor\right) + c\left(n^2+\left(\frac{n^2}{4^2} \right)+\left(\frac{n^2}{16^2} \right)\right) \leq \dots [/math] [math] \dots \leq 1+cn^2\cdot\left(\sum_{i=0}^{\left \lfloor log_4n \right \rfloor} \left (\frac{1}{16} \right )^i\right)[/math]
Azt kell észrevennünk, hogy ez tulajdonképpen egy mértani sor, amire van képletünk:
[math]\sum_{i=0}^{k} r^i = \frac{1-r^{k+1}} {1-r} [/math], ahol [math] k = \left \lfloor log_4n \right \rfloor, r = \frac{1}{16}[/math], vagyis [math]\frac{1-\frac{1}{16}^{\left \lfloor log_4n \right \rfloor+1}} {1-\frac{1}{16}}[/math]
[math]\frac{1-\frac{1}{16}^{\left \lfloor log_4n \right \rfloor+1}} {1-\frac{1}{16}} \lt 2 ,[/math]ha [math] n \geq 1[/math] (A lényeg, hogy felülről becsüljük!)
Tehát [math] T(n) = \dots \leq 1+2 \cdot cn^2=O(n^2)[/math]6. Feladat (Van megoldás)
Egy ország n kis szigetből áll. Szeretnénk néhány hajójáratot indítani a szigetek között úgy, hogy bárhonnan bárhova el lehessen jutni (esetleg átszállással). Ehhez ismerjük bármely két szigetre, hogy mennyibe kerül egy évben a hajójárat fenntartása közöttük, illetve azt, hogy mekkora az itt várható éves bevétel. Adjon algoritmust, ami ezen adatok ismeretében [math]O(n^2)[/math] időben meghatározza, hogy hol indítsuk el a hajójáratokat, ha a lehető legnagyobb várható éves hasznot (vagy a lehető legkisebb veszteséget) szeretnénk elérni. (Egy szigeten egy hajóállomás van csak).
- Első lépésben az élsúly legyen a [math] Profit = -(Bevetel - Kiadas) .[/math]
- Vegyük fel az összes profitot termelő, vagy legalábbis veszteséget nem termelő éleket [math] (Profit \geq 0 )[/math] [math] \Rightarrow O(n^2) [/math] lépés. Ez legyen mondjuk a G gráf.
- Két eshetőség áll fenn:
- Ha a G gráf összefüggő, akkor jók is vagyunk, nincs további teendőnk, meg is vagyunk.
- Ha nem összefüggő, akkor:
- Az egyes komponenseket tekintsük egy pontnak. Minden olyan él, ami ebbe a komponensbe megy, menjen ebbe a pontba. Így kapunk egy F gráfot.
- Erre az F gráfra hívunk meg egy Prim-algoritmust, ami [math] O(n^2) [/math] időben keres az F gráfban egy minimális feszítőfát (vagyis a komponenseket - ami most jelenleg 1-1 pont a gráfban - a lehető legkisebb költségű élekkel köti össze).
- Tehát Prim-algoritmussal, vagy anélkül [math] O(n^2) [/math] időben megmondjuk, hogy mely hajójáratok indításával lesz az évi bevétel a legmagasabb.
7. Feladat
TODO
8. Feladat
TODO